1; 2; 3; 6; 31; 62; 93; 186.
Пошаговое объяснение:
Если в разряде единиц стоит 1, то в разряде десятков будет 3*1=3.
Если в разряде единиц стоит 2, то в разряде десятков будет 3*2=6.
Если в разряде единиц стоит 3, то в разряде десятков будет 3*3=9
Дальше получаются 3-х значные числа.
итого, имеем 31, 62, 93.
31+62+93=186
расскладываем 186 на простые множители:
186:2=93
93:3=31 - простое число
31:31=1
Значит, 186=1*2*3*31
Данное число делится на 1; 2; 3; 31, а также на все возможные произведения этих чисел:
2*3=6
2*31=62
2*3*31=186
3*31=93
Проанализировав полученное уравнение, понимаем, что нулю оно равняется в двух случаях: когда первый множитель равен нулю или когда второй множитель равен нулю.
С первым все понятно: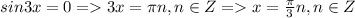
Теперь рассмотрим второй множитель: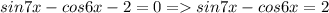
Так как функции sin и cos - это ограниченные функции, а именно не превышающие по модулю единицу, то такое равенство возможно тогда и только тогда, когда одновременно sin7x = 1, а cos6x = -1. Решим эти простые уравнения и найдем пересечение корней:
Теперь приравняем полученные результаты:
Заметим, что пара чисел k = 5 и m = 4 является решением, а значит, являются решением все числа вида:
Подставим это в любую серию корней и найдем пересечения (например, в первую):
На промежутке от![[0; 2\pi]](/tpl/images/1359/8514/9301a.png)
уравнение имеет 7 корней.
ответ: 7 корней