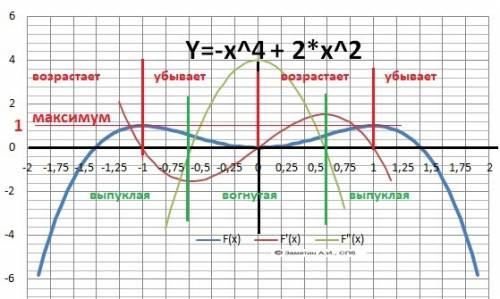
ДАНО: Y= - x⁴ + 2*x²
ИССЛЕДОВАТЬ с производных.
ДУМАЕМ силой разума - это парабола четвертого порядка с отрицательным коэффициентом - ветви вниз.
РЕШЕНИЕ
Y = - x²*(x² -2) = - x²*(x - √2)*(x + √2) - формула - разность квадратов.
1. Область определения - x∈R, X∈(-∞;+∞).
Вывод - непрерывная, разрывов - нет, вертикальных асимптот - нет.
И сразу ВИДИМ четыре корня функции.
2. Пересечение с осью Х - в корнях функции: х₁,₂ = 0, х₃ = -√2, х₄ =√2
(на график)
Интервалы знакопостоянства.
Отрицательна: Х∈(-∞;-√2)∪(√2;+∞)
Положительна: Х∈(-√2;0)∪(0;√2)
3. Первая производная - поиск локальных экстремумов.
Y'(x) = - 4*x³ + 4*x = -4*x*(x²-4) = -4*x(x-1)*(x+1) = 0.
Видим три корня производной: х₁ = -1, х₂ = 0, х₃ = 1.
Это уже кубическая функция и тоже с отрицательным коэффициентом.
Схема знаков: (-∞) >0 (-1) <0 (0) >0 (1) <0 (+∞) - это надо видеть.
4. Локальные экстремумы и монотонность.
Максимум: Y(-1) = 1, минимум: Y(0) = 0, максимум: Y(+1) = 1 - (на график)
Возрастает: Х∈(-∞;-1)∪(0;1) и убывает: Х∈(-1;0)∪(1;+∞)
5. Вторая производная поиск точек перегиба.
Y"(x) = -12*x²+ 4 = 0. x = +/- 1/√3 = +/- √3/3 ≈ 0.58
6. Выпуклая - "горка" - Х∈(-∞; -0.58)∪(0.58;+∞)
Вогнутая - "ложка" - Х∈(-0,58;0,58) - между корнями Y"(x).
1) а) x=-1
F(x)= -1 +1 / -1 = 0
f(x)=0
b) x=1/2
F(X)=1/2 +1 / 1/2
f(x)= 3
c) x=10
F(x)=10 +1 / 10
f(x) =11/10= 1.1
2) a )x=-pi/4
F(x)=3cos( -pi/4- pi/4)
F(x)= 3cos (-pi/2)
cos(+-pi/2)=0 => F(x)=0
b) X=0
F(x) = 3cos(0 - pi/4)
F(x)=3cos(-pi/4)
cos(+-pi/4)=корень из 2/2 => F(x)=3 корня из 2 /2
с)x=pi
F(x)=3cos(pi-pi/4)
F(x)=3cos(3/4pi)
f(x)= -3 корня из 2 /2