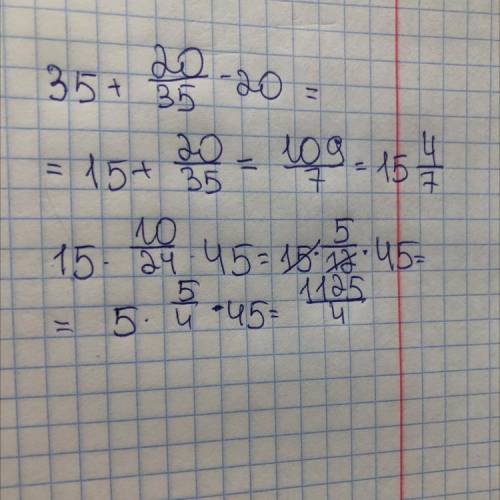
1/2; 5/6; 1/10; 2/5; 4/5; 3/8; 3/4;1/12;2/13;
1/7; 4/7; 2/13; 1/3; 4/5; 12/17; 2/3; 2/3;1/6;
3/8; 2/9; 4/5; 3/8; 4/7; 1/5; 2/3; 4/9;5/72;
1/11; 2/3; 2/3; 5/11; 2/3; 3/20; 1; 1/5; 2/11
Пошаговое объяснение:
6/12=1/2 (:6); 35/42=5/6 (:7); 6/60=1/10 (:6); 22/55=2/5 (:11); 8/10=4/5 (:2); 150/400=3/8 (:50); 12/16=3/4 (:4); 12/144=1/12 (:12); 58/377=2/13 (:29);
7/49=1/7 (:7); 16/28=4/7 (:4); 14/91=2/13 (:7); 18/54=1/3 (:18); 52/65=4/5 (:13); 600/850=12/17 (:50); 20/30=2/3 (:10);
144/216=2/3 (:72); 57/342=1/6 (:57);
36/96=3/8 (:12); 18/81=2/9(:9);24/30=4/5
(:6); 9/24=3/8 (:3); 8/14=4/7 (:2); 23/115=1/5 (:23); 50/75=2/3 (:25); 56/126=4/9 (:14); 115/1656=5/72 (:23);
5/55=1/11 (:5); 32/48=2/3 (:16); 10/15=2/3
(:5); 10/22=5/11 (:2); 20/30=2/3 (:10);
126/840=3/20 (:42); 4/4=1 (:4); 78/390=1/5 (:78); 88/484=2/11 (:44).
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -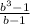
· X
После четвертой выплаты сумма оставшегося долга равна:
S4 =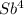 
- (1 + b +b² + b³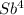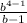)X = 
- 
· X
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому 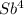- 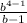· X = 0.
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X = 
рублей
Зайди в Photomatch там всё пошагово показано.
Пошаговое объяснение: