Находим стационарные точки
1) z'(x) = 0, z'(x)= 54x + 9y^2 -27
2) z'(y) = 0, z'(y) = 18xy + 6y^2 = 6y(3x + y) => y = 0 или 3x + y = 0 =>
1)a) подставляем y = 0 в первое: 54x - 27 = 0; x = 0,5
1)б) решаем систему из 54x + 9y^2 -27 = 0 и 3x + y = 0, из второго выражаем y: y = -3x и подставляем в первое: 54x + 81x^2 - 27 = 0 => x1 = -1, x2 = 1/3; y1 = 3, y2 = -1.
М1(0,5;0), М2 (-1; 3), M3 (1/3;-1).
z''(x) = 54
z''(xy) = 18y
z''(y) = 18x + 12y
1) Берем М1: z''(x)|M1 = 54 = A1; z''(xy)|M1 = 0 = B1; z''(y)|M1 = 9 = C1; D1 = A1C1 - B1^2 = 486 => D1 > 0, A1 > 0 => M1 - минимум
2) 1) Берем М2: z''(x)|M2 = 54 = A2; z''(xy)|M2 = 54 = B2; z''(y)|M2 = 18 = C2; D2 = A2C2 - B2^2 = -1944 => D2 < 0 => в M2 экстремума нет
3) Берем М3: z''(x)|M3 = 54 = A3; z''(xy)|M3 = -18 = B3; z''(y)|M3 = -6 = C3; D3 = A3C3 - B3^2 = -648 => D3 < 0 => в M3 экстремума нет
Сначала нужно перенести все неизвестные члены уравнения в одну сторону, а известные в другую.
Неизвестные это члены с переменными (х,y,a,b и т.д.)
При переносе знаки меняются, то есть если было х = 1, то будет х -1 = 0
Знак изменился у 1 с +1 на -1. (просто знак + перед числами принято не писать)
У нас получится: х - 8х = - 14
Или можно сделать так: 14 = 8x -x
Переносить можно в обе стороны, главное следить за знаком. Обычно делают так, что бы неизвестное было слева, но т.к. у нас все отрицательное, мы перенесем его вправо.
Мы имеем уравнение: 14 = 8x -x
Для удобства можно поменять их местами и получиться 8х - х = 14.
Теперь нужно привести подобные. У подобных слагаемых одинаковые буквенные части. То есть, если бы у нас было 2x+8y-2y+8x = 2х+8х+8y-2у = 10х + 6у
В нашем случае будет 8х - х = 7х.
(Если стоит просто х, то это можно считать как 1х, что бы было проще. И получается 8х - 1х = 7х. 8-1=7 и просто дописываем х)
Значит все уравнение будет иметь вид 7х = 14
Теперь, что бы найти х нужно поделить правую часть на основание при Х.
Тоесть поделить 14 на 7
х = 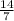
х = 2.
Теперь проверим. Подставим 2 вместо Х в изначальное уравнение.
2 = 8*2 - 14
2 = 16 - 14
2 = 2.
Решение верное.
находим точки удовлетворяющие условию
dz/dx=0
dz/dy=0
Частные производные от функции z равны
df/dx=d/dx(27x^2+9xy^2-27x+2y^3)=54x+9y^2-27
df/dy=d/dy(27x^2+9xy^2-27x+2y^3)=18xy+6y^2
Приравниваем их к нулю и решаем систему
54x+9y^2-27=0
18xy+6y^2=0
Из второго уравнения имеем
x=-y/3
подставив в первое уравнение получим
y^2-2y-3=0
Решая это квадратное уравнение получим два корня
y1=-1
y2=3
при y1=-1 имеем x1=1/3
при y2=3 имеем x2=3
А также при y=0 x=0,5
таким образом получили три точки
М1=(1/3; -1)
M2(-1; 3)
M3(0,5; 0)
Находим вторые производные
d/dx(df/dx)=d/dx(54x+9y^2-27)=54
d/dy(df/dx)=d/dy(54x+9y^2-27)=18y
d/dy(df/dy)=d/dy(18xy+6y^2)=18x+12y
далее для каждой точки M1 и M2 установим наличие экстремума
M1(1/3;-1)
A=d^2f/dx^2 |м1=54
B=d^2f/dx*dy |м1 =18*(-1)=-18
C=d^2f/dy^2 |M1 =18*1/3+12*(-1)=-6
Дискриминат=AC-B^2=54*(-6)-(-18)^2=-648 <0
так как дискриминат меньше нуля, то точка M1 не имеет ни минимумов ни максимумов
M2(-1 ;3)
A=d^2f/dx^2 |м2=54
B=d^2f/dx*dy |м2 =18*3=54
C=d^2f/dy^2 |M2 =18*(-1)+12*3=18
Дискриминат=AC-B^2=18*54-54^2=-1944<0
так как дискриминат меньше нуля, то точка M2 не имеет ни минимумов ни максимумов
M3(0,5; 0)
A=d^2f/dx^2 |м3=54
B=d^2f/dx*dy |м3 =18*0=0
C=d^2f/dy^2 |M3 =18*(0,5)+12*0=9
Дискриминат=AC-B^2=54*9-0^2=486>0
так как дискриминант >0 и А>0, то функция z имеет min в точке M3(0,5; 0)
Zmin=27x^2+9xy^2-27x+2y^3=27*(1/2)^2+9*0,5*0^2-27*1/2+2*0^3=
27/4-27/2= -6,75