В первый аквариум вмещается больше воды.
Пошаговое объяснение:
Данные аквариумы имеют форму прямоугольного параллелепипеда. Надо сравнить объёмы этих параллелепипедов.
Объём прямоугольного параллелепипеда определяется по формуле:
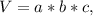 где a,b, c - измерения прямоугольного параллелепипеда( длина, ширина, высота)
где a,b, c - измерения прямоугольного параллелепипеда( длина, ширина, высота)
По условию у первого аквариума
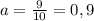 м ;
м ;
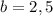 м;
м;
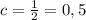 м.
м.
Тогда объем
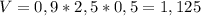 м³
м³
У вторго аквариума
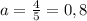 м;
м;
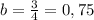 м;
м;
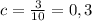 м.
м.
И объём второго аквариума будет
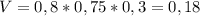 м³
м³
Так как 1,125 м³ > 0,18 м³, то в первый аквариум вмещается больше воды.
Пусть х - это длина одной стороны, тогда длина второй стороны будет равна (8-х)
Пусть у - площадь этого прямоугольника,
тогда у=х(8-х)
Требуется найти значение х, при котором у принимает максимальное значение
у=-х*х+8х график этой функции - парабола, у которой ветви направлены вниз и пересекают ось абцисс в точках, т.е. у=0, х=0 ; у=0, х=8
Значит максимум находится в вершине этой параболы. Значит х=4, а следовательно
одна сторона этого прямоугольника равна 4, а вторая сторона 8-4=4, это квадрат.
ответ: каждая стороны этого прямоугольника равна 4 метрам.
пусть искомое число х, а 75% - это 3\4 числа. составим выражение
8\9х - 3\4х = 180
решим его
х * (32\36 - 27\36) = 180
х * 5\36 = 180
х = 180 / 5\36
х = 1296