Пусть N имеет натуральные делители и их сумма равна A. Пусть, кроме того, где N - нечетное число.
Четные делители числа N имеют вид
Складывая четные делители группами в соответствие с тем, сколько множителей вида 2 в них есть, а потом складывая эти группы, получим
Требуется проверить, может ли
быть полным квадратом, то есть равняться B².
Конечно, такого быть не может, так как если перенести 1 направо, мы получили бы
Выражение, стоящее слева, делится на 2, но не делится на 4, выражение же, стоящее справа, или является нечетным (если B четное), или же делится не только на 4, а даже на 8 (хотя нам это и не нужно) -- ведь из двух последовательных четных чисел одно обязательно делится на 4.
1) 20 + 15 = 35 (д) - на столько деревьев больше посадили на 1-й и 3-й аллеях чем на 2-й 2) 80 - 35 = 45 (д) - столько деревьев было бы на всех трех аллеях, если бы на каждой посадили одно и то же количество деревьев 3) 45 : 3 = 15 (д) - столько деревьев посадили на 2-й аллее 4) 15 + 20 = 35 (д) - столько деревьев посадили на 1-й аллее 5) 15 + 15 = 30 (д) - столько деревьев посадили на 3-й аллее
Либо можно решить через х
Пусть х- вторая аллея То первая будет х+20 , а третья х+15. Составим уравнение: Х+20+х+х+15=80 3х+35=80 ( сократили) 3х=80-35=45 Х=45:3=15. - на второй аллее 15+20=35- на первой 15+15=30 - на третьей
Пусть N имеет натуральные делители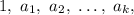
и их сумма равна A. Пусть, кроме того, 
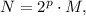где N - нечетное число.
Четные делители числа N имеют вид
Складывая четные делители группами в соответствие с тем, сколько множителей вида 2 в них есть, а потом складывая эти группы, получим
Требуется проверить, может ли
быть полным квадратом, то есть равняться B².
Конечно, такого быть не может, так как если перенести 1 направо, мы получили бы
Выражение, стоящее слева, делится на 2, но не делится на 4, выражение же, стоящее справа, или является нечетным (если B четное), или же делится не только на 4, а даже на 8 (хотя нам это и не нужно) -- ведь из двух последовательных четных чисел одно обязательно делится на 4.