2
Объяснение:
1-е базовое, 2-е сервисное
бабочки рождаются чтобы умереть,дав жизнь следующему поколению.большая часть из них,живет всего несколько дней.
они являются вторыми почислености опылителями после пчел.
бабочки пробуют еду стоя на ней,потому что их датчики вкуса находятся в ногах.
скорость полета бабочек,достигает свыше 60км в час.
наука о бабочках называется-лепидоптерология.
за свою столь короткую жизнь самка бабочки может отложить больше 1000 яиц.
некоторые бабочки при нападение на них хищников,притворяются мертвыми.
бабочки не шлышат,но они чувствуют вибрацию
Это сумма бесконечно убывающей геометрической прогрессии. У нее есть формула для вычисления.
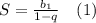
Здесь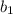 
- первый член бесконечно убывающей геометрической прогрессии. В данном случае он равен 0,5.
q - знаменатель бесконечно убывающей геометрической прогрессии. В данном случае он равен отношению каждого последующего члена прогрессии к предыдущему члену.
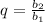
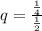
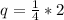
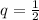
Подставим в формулу (1) все значения.
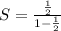
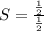
S=1.
В данном случае n - какое-то конечное число, а сумма взята в случае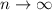 
.
То есть при любом конечном n, данная сумма всегда будет меньше 1.
2
Пошаговое объяснение:
Существует два основных типа программного обеспечения: системное (называемое также общим) и прикладное (называемое специальным). Каждый тип программного обеспечения выполняет различные функции.