Чтобы из числа можно было сделать все шесть различных двухзначных чисел, необходимо, чтобы исходное число было трехзначным и все цифры в нем были разные, представим это число в виде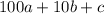 
.
А сумма всех шести различных двухзначных чисел будет такая:
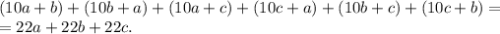
При этом (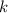
натуральное):
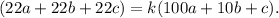
Представим теперь, что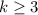 
, то есть:
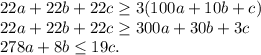
Но это противоречие, так как правая часть по-любому больше левой, а здесь она меньше. Поэтому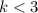 
.
Итак, нужно рассмотреть два случая:
1). 
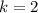. Тогда:
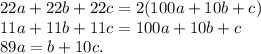
Нетрудно понять, что в натуральных однозначных числах здесь всего одно решение: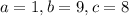 
.
А нужное число - это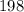 
.
2). Случай посложнее: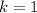 
.
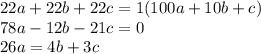
Если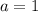 
уравнение принимает вид 
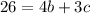, и, тогда в вышеуказанных условиях у него такое одно решение: 
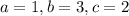. Число - 
.
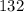Ну а теперь пусть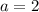 
и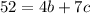 
. Здесь методом подбора: 
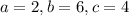. А число - 
.
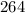И последний случай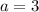 
, то есть 
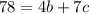, где, подбором, 
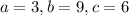. Число 
.
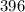Делаем вывод, что Вася богатый и у него в доме четыре (по крайней мере!) квартиры.
1. (а + b)¹= а + b 2. (а + b)²= а²+ 2аb + b² 3. (а + b)³= а³ +3а²b + 3аb² + b³ Можно раскрыть скобки при вычислении (а +b) и т.д., умножая полученный.Содержание. 1) Понятие бинома Ньютона. 2) Свойства бинома и биномиальных коэффициентов. 3) Примеры решения задач по теме «Бином Ньютона». 4) Выход.Глава 9. Элементы математической статистики, комбинаторики и теории вероятностей §53. Формула бинома Ньютона.БИНОМ НЬЮТОНА. Определение. Двучлен вида a+b называют биномом.Автор : Ван – Хо – Син Виктория Петровна, 7А класс. МОУ СОШ7 г.Амурска. Бином Ньютона.11 класс МКОУ «Усть-Мосихинская СОШ» Новосёлова Е.А.N!n! Волошина Н.Н., Произведение биномов, отличающихся только вторыми членами. Выражение х + а, как и вообще всякий двучлен, называется.Бином Ньютона Бином bis дважды nomen часть Натуральную степень двучлена умели представлять в виде суммы степеней его слагаемых еще в 10 веке индийцы.Бином Ньютона Бином bis дважды nomen часть Натуральную степень двучлена умели представлять в виде суммы степеней его слагаемых еще в 10 веке индийцы.
((169,68:5 3/5-22 4/5)*9 2/5+9,7)*22,=
Действие 1)169,68 / 5⅗=169,68 / 5,6=30,3 (предварительно 5⅗ мы перевели в десятичную дробь ,умножив ⅗ на 2)
2)30,3 - 22 4/5=30,3-22,8=7,5 (предварительно 4/5 мы перевели в десятичную дробь)
3)7,5 * 9⅖=7,5* 9,4=70,5 (предварительно ⅖ мы перевели в десятичную дробь)
4)70,5+9,7=80,2
5)80,2*22,5=1804,5