Пошаговое объяснение:
y'+2xy'+2y=1
Представим в виде:
2xy'+2y+y' = 1 - это неоднородное уравнение.
Сделаем замену переменных: y=u*v, y' = u'v + uv'.
2·u·v+u·v'+u'·v+2·x·(u·v'+u'·v) = 1
Выберем переменную v так, чтобы выполнялись условия:
1. u(2·v+2·v'·x+v') = 0
2. 2·u'·v·x+u'·v = 1
1. Приравниваем u=0, находим решение для:
2·v+2·v'·x+v' = 0
Представим в виде:
v' = -2·v/(2·x+1)
Преобразуем уравнение так, чтобы получить уравнение с разделяющимися переменными:
Интегрируя, получаем:
ln(v) = -ln(2·x+1)
v = 1/(2·x+1)
2. Зная v, Находим u из условия: 2*u'*v*x+u'*v = 1
2·u'·x/(2·x+1)+u'/(2·x+1) = 1
u' = 1
Из условия y=u*v, получаем:
y = u·v = (C+x)/(2·x+1)
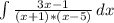
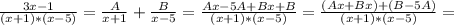
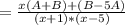
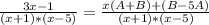
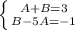
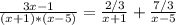
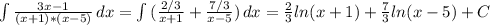
0.5 пути проехал
х-скорость пешком
v t s
ехал на транс. 10х 0,05х 0.5
волах х:2 1:х 0,5
шёл х 1:х 1
10х*0.05х+х:2*1:х=х*1:х
10*5х*х/100+0.5=1
х*х/2=1-0.5
х*х=0.5
х*х/2=0.5/1
х*х=1*2/2
х*х=1
значит х =1
1*1=1
потом подставляешь в таблицу всё так и выйдет
время езды складываешь(на волах и транспорте) и вычитаешь время пешком =
1,05-1=0,05=3 минуты
он выгадал 0.05 часа=60*0.05=3минуты