Былины - русские народные эпические песни. Они повествуют о подвигах богатырей, сражающихся с чудовищами или вражеским войском, отправляющихся в загробный мир или еще каким-либо образом проявляющих свою силу, удаль, храбрость. В детстве все узнают об Илье Муромце и других богатырях, которые скоро перемешиваются с персонажами сказок, а с возрастом просто забываются как "детские". А между тем былины вовсе не принадлежали к детскому фольклору. Напротив, эти песни исполнялись взрослыми серьезными людьми для таких же взрослых серьезных людей. Переходя от поколения к поколению, они служили передачи древних верований, представлений о мире, сведений из истории. А все, о чем рассказывается в былинах, воспринималось как правда, как реально происходившие когда-то в далеком события. Собственно народное название былины - старина, т. е. повествование о старинных событиях. Слово "былина" впервые употребил для обозначения этого жанра в середине века собиратель и исследователь фольклора И. П. Сахаров. Традиционно выделяются два цикла былин, объединенные по месту действия или происхождению героев:
1. Киевские или Владимировы былины (песни об Илье Муромце, Добрыне Никитиче, Алеше Поповиче и др.) . 2. Новгородские былины (Герои - Садко и Василий Буслаевич) .
Кроме того, существует ряд песен, не входящих ни в один из этих циклов. Былинные богатыри Главные герои былин - богатыри, люди исключительные, наделенные чертами, которыми не обладает обычный человек: невиданной силой, безграничной храбростью, особенным умением или талантом. Так, если Илья Муромец знаменит своей силой, то Садко - своим непревзойденным искусством играть на гуслях. Среди богатырей принято выделять "старших" и "младших". К "старшим", как правило, относят Святогора и Волха Всеславьича. "Старшие" богатыри называются так не только потому, что они по возрасту старше других витязей, но и потому, что они представляют собой более древний, архаичный тип героя. Такому герою нет равного на земле, он единственный в своем роде, так что у него не может быть противника, кроме самой природы, матери-сырой земли. Бесспорно, черты этих богатырей сказочны. Поступки, ими совершаемые, обстоятельства, в которых они действуют, совсем не похожи на реальные события. Зато в их образах ярче, чем в других случаях, просматриваются древние мифологические представления. Часто повторяющийся в былинах сюжет - сватовство. Богатырь, чтобы найти себе невесту, обычно отправляется в чужое царство, в дальний путь. По дороге герою приходится преодолеть много преград и совершить множество подвигов. Невеста, как и сам богатырь, часто обладает каким-либо особенным свойством. Значительная часть былин посвящена борьбе богатыря с чудищем или вражеской силой. Былинный богатырь, как правило, действует в одиночку, идет навстречу страшной опасности и всегда в итоге побеждает. Однако помимо желания проявить свою удаль и потешить "богатырско сердце" героями былин движет и желание постоять за людей и за веру. Их противники несут беду людям - похищают, убивают - и ведут себя нечестиво. Садко и Василий Буслаевич Новгородские былины носят несколько иной характер. В них нет "могучих богатырей", "полениц удалых", сражающихся с вражьей силой. Герои этих песен - Садко и Василий Буслаевич, как и киевские богатыри, обладают яркими и особенными чертами: Садко прекрасно играет на гуслях. Садко отличается от обычных людей и тем, что путешествует на дно морское и удачно возвращается. Василий Буслаевич обладает невероятной силой, которой никто не может противостоять. Однако применяет силу Василий не для борьбы с чудищами или вражьей нечистью, а для собственного развлечения. Сюжеты былин часто связаны с нарушением героем какого-либо запрета. Нарушение запрета или просто дерзость сулят героям беду. Это связано с тем, что все происходящее в песне, все, что приходится выполнять ее персонажам, предопределено. Какая-то высшая сила - Бог, судьба - решает, что должно случиться!
1. В основании призмы лежат - многоугольники.
2. Боковые рёбра призмы - перпендикулярны основаниям.
3. Призма имеет 30 граней. В её основании лежит (какой многоугольник) - многоугольник в 28 углов, 84 рёбер, 56 вершин.
(Боковых граней 30-2=28. Значит это 28-угольник. Вершины = 28×2, рёбра = 28×2+28)
4. Диагональю призмы называется - отрезок, концами которого служат две вершины призмы, не лежащие на одной ее грани.
5. Прямоугольным параллелепипедом называется - прямая призма, основанием которой является прямоугольник.
6. Призма называется наклонной, если - ее боковые ребра не перпендикулярны основаниям.
7. Призма называется правильной, если - основанием которой является правильный многоугольник.
8. Площадью полной поверхности призмы называется сумма - всех боковых граней призмы.
9. Все двугранные углы при боковых гранях прямой призмы - прямые.
10. Площадь боковой поверхности куба с ребром 10 см равна - 600 см².
( так как у куба 4 боковых стороны и 2 основания, т.е. всего 6 квадратных сторон. А площадь одной стороны считается по формуле:
S = a², где а - длина стороны квадрата.
S = 10×10 = 100 см². - площадь одной стороны квадрата.
Тогда площадь всей поверхности куба:
S куба = 6×S
S куба = 6×100 = 600 см²).
11. Площадь полной поверхности куба с ребром 6 см равна - 216.
(так как грани куба - квадраты, площадь каждого квадрата равна
6² = 36. Куб состоит из шести таких квадратов значит площадь полной поверхности равна 36×6 = 216).
12. Площадь боковой поверхности правильной четырёхугольной призмы с высотой h и стороной основания a равна - Sб.п.= 4ah
13. Если диагональ куба равна d, то площадь полной поверхности куба равна - 2d²
(Так как S полy. пов. куба равна 6a² (а - ребро куба) ,
квадрат диагонали равен сумме квадратов всех измерений, тогда:
d²=3a² , тогда:
Sп.п. = 6a² = 2×(3a²) = 2d² )
14. Прямоугольный параллелепипед имеет три измерения, равные a=5 см, b=8 см, h =10 см. Площадь его полной поверхности равна - 340 см²
(Так как Sполн.пов. = Sбок. + 2Sосн.
Sбок. = Pосн. ×, S = 2×(5 + 8)×10 = 260 см²
Sосн. = а×в, S = 5×8 = 40 см²
Sполн. = 260 + 2×40 = 340 см²)
15.Площадь полной поверхности правильной треугольной призмы со стороной основания а и боковым ребром с равна - a²×√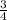 ×c = a²×c×√
×c = a²×c×√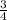
( Так как площадь основания равностороннего треугольника со стороной а = Sосн.= a²×√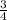
Таких оснований у призмы две.
Sбок.грани прямоугольника=
Sбок.гр. = a×c, таких граней три.
Sполн.пов. =
Sп.п. = 2×Sосн.+ 3×Sбок.гр. = a²×√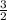 + 3ac
+ 3ac
Объем призмы =
V = Sосн.×H = a²×√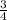 ×c = a²×c×√
×c = a²×c×√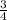 ).
).