Question

Доказать, что , где p - простое число, делится на 24

Answer 1

при р=2 или р=3 - утверждение неверно

при простом р>3 любое простое число имеет вид либо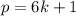 $p=6k+1$, где k  -  некоторое действительное число, либо 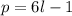$p=6l-1$, где l  -  некоторое действительное число

(используя формулу квадрата двучлена)

1 случай

$p^2-1=(6k+1)^2-1=(6k)^2+2*(6k)+1^2-1=36k^2+12k+1-1=36k^2+12k=12k(3k+1)$

очевидно, що выражение делится на 12( один из множителей делится на 12)

из двух чисел k и 3k+1 одно обязательно делится на 2 (так как они разной четности)

а значит выражение делится на 12*2=24, что и требовалось доказать

Доказано

2случай

$p^2-1=(6l-1)^2-1=(6l)^2-2*(6l)+1^2-1=36l^2-12l+1-1=36l^2-12l=12l(3l-1)$

очевидно, що выражение делится на 12( один из множителей делится на 12)

из двух чисел l и 3l-1 одно обязательно делится на 2 (так как они разной четности)

а значит выражение делится на 12*2=24, что и требовалось доказать

Доказано

Доказано

прим. (При делении на 6 возможны остатки 0, 1,2,3,4,5,6

значит любое целое число можно записать одним из видов 6k, 6k+1, 6k+2, 6k+3, 6k+4, 6k+5,

при єтом 6k, 6k+2=2*(3k+!), 6k+3=3*(2k+1), 6k+4=2*(3k+2) - не будут простыми)

прим 2. (6l-1=6(m+1)-1=6m+6-1=6m+5)