
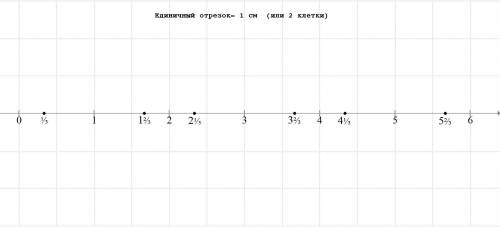
Надо нарисовать числовой луч и отметить на нём сначала целые числа (здесть можно от нуля до шести), а затем указанные точки (они как раз поместятся в диапазон от нуля до шести).
Если взять за единичный отрезок 1 сантиметр (это 2 клетки в обычной тетради в клеточку), то все эти дроби можно отметить, мысленно поделив на три части нужный сантиметровый отрезок, и взяв одну или две таких части (для дроби 1/3 либо 2/3).
Как это выглядит- смотри на первом рисунке внизу.
Если же брать за единичный отрезок три тетрадных клетки (это 1,5 см), то тогда эти же дроби можно отметить точно по клеточкам (правда луч при этом получится чуть длиннее).
Результат- смотри на втором рисунке внизу.

ответ: 3
Пошаговое объяснение:
Пусть а - ребро куба (СD = АD = CC1 = a) , АС1 - диагональ куба.
Проведем АС - диагональ основания (см.рисунок).
СС1 перп. СД и ВС (т.к все грани представляют собой квадрат), => СС1 перп. всему нижнему основаниваю, т.е перпендикулярно любой прямой, лежащей в плоскости основания).
Отсюда следует, что СС1 перп. АС, => АСС1 - прямоугольный треугольник.
Рассм. треугольник АСС1 - прям.:
угол С = 90°, СС1 = а, АС1 = 3√3, АС = а√2 (по св-ву диагоналей квадрата или по т. Пифагора из треугольника АСD).
Составим следующее уравнение из т. Пифагора для тр. АСС1:
(3√3)² = а² + (а√2)²
27 = 3а²
а² = 9
а1 = 3
а2 = -3 (т.к мы ищем ребро, нам нужна положительная величина)