3757 | 13 289 | 17
289 | 17 17 | 17
17 | 17 1
1 289 = 17²
3757 = 13 · 17²
НОК (3757 и 289) = 13 · 17² = 3757 - наименьшее общее кратное
3757 : 289 = 13 - число 3757 кратно числу 289
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
623 | 7 16821 | 3
89 | 89 5607 | 3
1 1869 | 3
623 = 7 · 89 623 | 7
89 | 89
1
16821 = 3³ · 7 · 89
НОД (623 и 16821) = 7 · 89 = 623 - наибольший общий делитель
16821 : 623 = 27 - число 623 является делителем числа 16821
Пошаговое объяснение:
Вспомним формулу для определенного интеграла
Где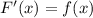 или
или 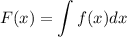 причем без константы!
причем без константы!
Вспомним также несколько формул
Так же понадобится формула производной корня из х
Нужна будет формула интегрирования по частям
Буду делать по действиям
НОМЕР 1
1 Решим сначала неопределённый интеграл, а затем вычислим определённый по формуле
2 Запишем 1 в интеграле как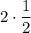
3 Вынесем 2 за знак интеграла как константу
4 Запишем внутри интеграла произведение двух дробей по-другому
5 Умножим все на (-1)(-1)
6 Вынесем -1 как множитель
7 Заметим, что первая дробь - производная квадратного корня, запишем
8 Объединим в одну дробь
9 Подведем корень под знак дифференциала
10 Сделаем замену. Пусть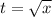
11 Запишем как степень
12 Умножим все на (-1)(-1)
13 Выносим -1 за знак интеграла
14 Заметим производную (-t) и внесем ее под знак дифференциала
15 Снова сделаем замену. Пусть s = -t
16 Ура! Табличный интеграл записываем формулу без константы, так как в определенном интеграле она не требуется
17 Сделаем обратную замену s = -t
18 Снова сделаем обратную замену,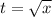
19 Запишем формулу определённого интеграла, учитывая что а у нас это 9, а b у нас это 4 (я уже поменял их местами из-за минуса в начале)
20 Посчитаем корни в степенях
21 Вынесем общие множители
22 Посчитаем
23 Умножим и получим ответ
И ЭТО ОТВЕТ
НОМЕР 2
1 Опять запишем неопределённый интеграл
2 Запишем 1 как произведение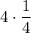
3 Вынесем ¹/₄ за знак интеграла
4 Заметим производную экспоненты, внесем ее под знак дифференциала
5 Применим формулу интегрирования по частям
6 Снова запишем 1 как произведение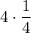
7 Снова вынесем ¹/₄ за знак интеграла
8 Заметим производную 4х и внесем ее под знак дифференциала
9 Сделаем замену t = 4x
10 Табличное значение! Запишем
11 Сделаем обратную замену
12 Запишем формулу определённого интеграла
13 Посчитаем
И ЭТО ОТВЕТ
P.S. Я очень устал, попытался все максимально понятно вам объяснить (в задании написано "я их совсем не понимаю") Если остались вопросы, задавайте