

Вероятность того, что случайно взятый код содержит последовательность 123, равна отношению количества кодов, содержащих последовательность 123, к общему количеству кодов.
Так как коды составляются путем перестановок из десяти цифр, то их общее количество равно числу перестановок из 10:
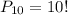
Так как нас интересует последовательность 123, то вместо цифр 1, 2, 3 будем сразу рассматривать эту последовательность. Итого имеем элементы: 0, 123, 4, 5, 6, 7, 8, 9. то есть всего 8 элементов. Общее количество кодов, которые можно получить, переставляя эти элементы, равно числу перестановок из 8:
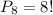
Таким образом, вероятность:
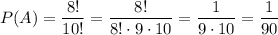
ответ: 1/90
Многочле́н (или полино́м от греч. πολυ- «много» + лат. nomen «имя») от {\displaystyle n}n переменных {\displaystyle x_{1},x_{2},...x_{n}}{\displaystyle x_{1},x_{2},...x_{n}}— это сумма одночленов или, строго, — конечная формальная сумма вида
График многочлена 7 степени.
{\displaystyle \sum _{I}c_{I}x_{1}^{i_{1}}x_{2}^{i_{2}}\cdots x_{n}^{i_{n}}}\sum _{I}c_{I}x_{1}^{{i_{1}}}x_{2}^{{i_{2}}}\cdots x_{n}^{{i_{n}}}, где
{\displaystyle I=(i_{1},i_{2},\dots ,i_{n})}I=(i_{1},i_{2},\dots ,i_{n}) — набор из {\displaystyle n}n целых неотрицательных чисел, именуемый мультииндексом,
{\displaystyle c_{I}}c_{I} — число, именуемое коэффициентом многочлена, зависящее только от мультииндекса {\displaystyle {\mathit {I}}}{\displaystyle {\mathit {I}}}.
В частности, многочлен от одной переменной есть конечная формальная сумма вида
{\displaystyle c_{0}+c_{1}x^{1}+\dots +c_{m}x^{m}}c_{0}+c_{1}x^{1}+\dots +c_{m}x^{m}, где
{\displaystyle c_{i}}c_{i} — фиксированные коэффициенты,
{\displaystyle x}x — переменная.
С многочлена выводятся понятия «алгебраическое уравнение» и «алгебраическая функция».
Пошаговое объяснение: