
Это простейшие производные.
Рассмотрим общий случай:
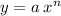
а – просто коэффициент при Х, n – степень Х.
Производная функции у, обозначаемая обычно у' или dy/dx, будет иметь следующий вид:
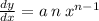
Ничего сложного.
Рассмотрим несколько частных случаев из Ваших примеров.
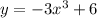
Здесь коэффициент а равен (–3), степень n равна 3. Значит, по правилу, представленному выше, производная будет иметь вид:
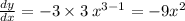
При числе 6 нет «Х», поэтому при взятии производной это число просто пропадает.
Другой частный пример:
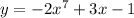
Берём производную от каждой части по отдельности.

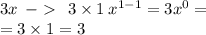

Итого:
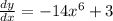
1) Продолжение фразы: Математическая дробь может быть использована как часть пропорции. (а/в=1/3)
Математическая дробь может быть использована как замена процентов. (25% = 25/100 = 1/4)
2) Предложения из 5 слов про дроби:
Дробь – часть (или несколько) целого (1:5*2=2/5)
Дроби нужны для перевода величин. (1 Гкал = 4,2 ГДж)
Курс обмена валют – десятичная дробь. (Курс доллара – 73,63 рубля)
Дробью измеряются площади сельскохозяйственных угодий (сотка это и 100кв.м и 1/100 часть гектара.)
Дроби применяются для вычисления времени (3/4 часа =45мин, квартал =1/4 года)
Дроби нужны для деления целого (в быту – суп на порции)
Дроби нужны для нахождения числа. (число, 2/3 которого равны 1000, это 1500)
Одни величины выражаются дробями других (1мм = 1/100м)
Результаты очков конкурсантов – часто дробные. (9, )
Процент магазинной скидки – это дробь. ( 20% скидки от 300 рублей –это уменьшение на 1/5, на 60 рублей)
Рукав три четверти – это дробь ( мода)
Пол-царства в сказках – это дробь! (литература)
Четвертушка блокадного хлеба – это дробь. (жизнь)
3) Науки где применяются дроби:
Агрономия, Антропология, Астрономия, Археология, , Биология, Геология, География, История, Кораблестроение, Космонавтика, Математика, Материаловедение, Машиностроение, Медицина, Механика ,Нанотехнология, Педагогика, Пищевые технологии и Кулинария, Политология , Радиотехника, Социология, Строительство и Архитектура, Теплотехника, Физика, Химия, Экономика
Трудно найти, где НЕ применяется дроби!