1) Пусть это верно. Тогда рыцари всегда говорят да, а лжецы - нет.
Значит надо найти максимальное количество рыцарей при верном условии.
Тогда лжецов минимальное количество. Найменьшее количество лжецов будет тогда, когда в четырех шеренгах лжецов 3, а в остальных шеренгах лжецов нет.
Тогда рыцарей 4*2+2*5=18
2) Псть это неверно. Тогда рыцари говорят нет, а лжецы говорят да. Значит надо найти максимальное количество ожецыв при неверном условии. Максимально их будет тогда, когда в трех шеренгах все - лжецы, а остальных шеренгах лжецов 2. Тогда их общее количество равно 3*5+3*2=21
21>18
ответ: 21
я хорошо вопроса не поняла но всё же я всегда пользуюсь традиционным методом решения в столбик))
1000/100
Я вам нарисую))
когда мы тысячу делим на сто, у нас сначала в столбику выходит ответ 1, и мы отнимает от первых трёх цифр в нашем случае это 100 число на которое делим. Вычитаем.У нас получилось 0. В ответе у нас уже имеете число один и в уменьшаемом остаётся 0. Этот ноль мы переносим в ответ. и получается 10.
Этот был самый простой пример, просто не могу найти чило 3-ёх значное, которое делится на 2345, напишите в сообщение число посложнее вместе с вычитаемым и вам объясню ещё подробнее:)
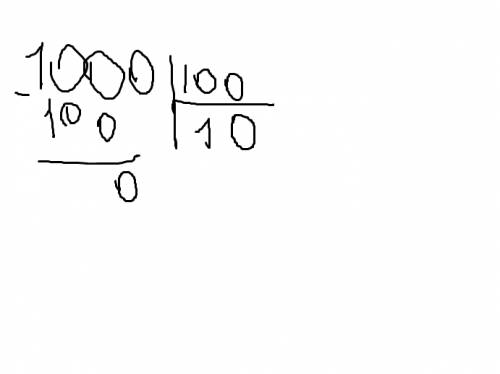
а)x=1 или x=-1; в) нет решений
Пошаговое объяснение:
а) есть 2 случая:
1) 2lxl+3=5
lxl=(5-3)/2=1
x=1 или x=-1
2)2lxl+3=-5
lxl=(-5-3)/2=-4
Однако по определению модуля, он всегда положительный. Этот случай не подходит. Остается x=1 или x=-1
в) Аналогично с предыдущим пунктом, есть 2 случая:
1)2lxl+3=1
lxl=(1-3)/2=-1, что невозможно;
2)2lxl+3=-1
lxl=(-1-3)/2=-2, что тоже невозможно;
следовательно, в этом случае данное уравнение не имеет решений.