3)) { 2- 1 7/12 } : { 3/8 - 1/6} • 3 1/4=
6 1/2= 6,5.
1)) 2- 1 7/12= 1 12/12- 1 7/12= 5/12
2)) 3/8- 1/6= (3•3)/(8•3)- (1•4)/(6•4)=
9/24 - 4/24= 5/24
3)) 5/12: 5/24• 3 1/4=
5/12• 24/5• (3•4+1)/4=
{сокращаем 5 и 5 на 5; 12 и 24 на 12}
1/1• 2/1• 13/4=
{сокращаем 2 и 4 на 2}
1/1• 1/1• 13/2= 13/2= 6 1/2= 6,5.
4)) {7/10 - 2/5} • {1/4+ 5/6} : 6 1/2=
1/20= 0,05
1)) 7/10- 2/5= 7/10- (2•2)/(5•2)=
7/10- 4/10= 3/10
2)) 1/4+ 5/6= (1•3)/(4•3)+ (5•2)/(6•2)=
3/12+ 10/12= 13/12
3)) 3/10• 13/12 : 6 1/2=
{сокращаем 3 и 12 на 3}
1/10• 13/4: (6•2+1)/2=
1/10• 13/4: 13/2=
1/10• 13/4• 2/13=
{сокращаем 13 и 13 на 13; 4 и 2 на 2}
1/10• 1/2• 1/1= 1/20= 0,05.
Пошаговое объяснение:
Пошаговое объяснение:
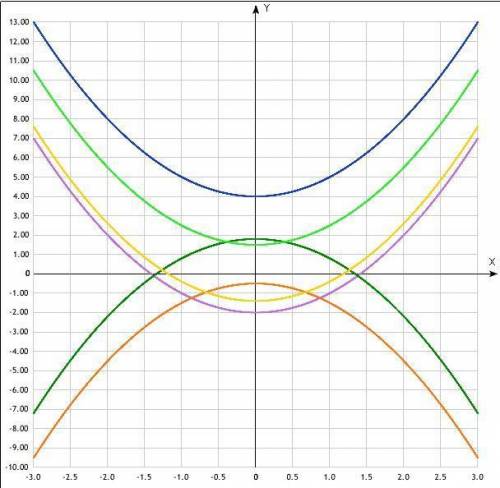
Все функции - параболы вида
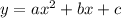
a - определяет "ширину" ветвей, при 0<а<1 ветви "шире", при а > 1 "уже"
При отрицательном а - ветви направлены вниз, при положительном вверх. В 3 и 4 примерах а = -1, поэтому ветки вниз
b - (в данных примерах не используется) показывает смещение вершины параболы вдоль оси OX, положительный левее, отрицательный правее от оси OY
с - смещение вершины графика вдоль оси OY - положительный с - выше, отрицательный ниже, при с=0 ветка графика пересекает точку 0,0
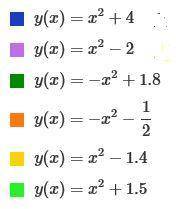
1)17+20=37
2)37:5=7,4