3.1
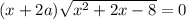
ОДЗ :
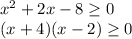
+ - +
-----------[-4]------------[2]---------------
x ∈ (-∞ ; -4] U [2 ; +∞)
Решим систему :
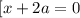
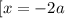
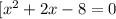
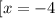
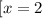
Уравнение будет иметь ровно два корня, если значение -2а не будет входить в ОДЗ или будет равняться значению -4 или 2. То есть если будет входить в промежуток [-4 ; 2]
Подставим конечные значение промежутка :
-2a = -4
a = 2
----------
-2a = 2
a = -1 - наименьшее значение
_________________________________
Уравнение будет иметь три корня, если значение -2а входит в ОДЗ и не равняется значению -4 и 2. То есть если будет входить в промежуток (-∞ ; -4) U (2 ; +∞).
Самое наименьшее натурально значение а, которое входит в данный промежуток, это а = 3
1. Наименьшее значение а, при котором уравнение имеет два корня: a = -1
2. Наименьшее натуральное значение а, при котором уравнение имеет три корня: a = 3
4.3
![(a^{2} -16)\sqrt[8]{x} = a+4](/tpl/images/1359/0078/fb245.png)
ОДЗ : x ≥ 0
Для начала рассмотрим 2 случая, когда а = 4 и а = -4
1. При а = 4 : 0 = 8 , x ∈ ∅
2. При а = -4 : 0 = 0, x ∈ [0 ; +∞)
Теперь мы можем поделить обе части уравнения на (a^2-16) :
![(a^{2} -16)\sqrt[8]{x} = a+4 | : a^{2} -16](/tpl/images/1359/0078/43567.png)
![\sqrt[8]{x} = \frac{a+4}{(a+4)(a-4)}](/tpl/images/1359/0078/af9ad.png)
![\sqrt[8]{x} = \frac{1}{a-4}](/tpl/images/1359/0078/22062.png)
Уравнение будет иметь корни, если правая часть будет больше или равно 0 :
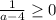
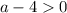
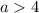
Уравнение будет иметь корни, если а ∈ (4 ; +∞) U {-4}
Наименьшее натуральное значение а, которое входит в данный промежуток, это а = 5
ответ : при а = 5
2. -5/6*11/3 = (-55/18) = -3 целых и 1/18 (знаменатель на знаменатель, числитель на числитель)
3. 17/8*(-4/5)= (-1,7)
4. -3/5*(-5/7) = 3/7
5. 7,8*(-2/3)= (-5,2) (7,8 превращаем в неправильную дробь (7*10+8 )/10 = 78/10)
6. x:5=-1.4
х=-1,4 * 5
х = (-7)
7. х:(-2/3)=11/6
х= 11/6 * (-2/3)
х = (-22/18) = -1 целая и 2/9
8. х:(3,5) = -11/7
х = -11/7 * 3,5
х = (-5,5)
9. 4/15*(-9/16)-3 целых 2/15 = (-3/20) - 3 целых 2/15 = (-9/60) - (188/60)=(- 3 целых 17/60)
10. -5/8 * 4/15 + 4 целых 1/9 = (-1/6)+37/9 = (-9/54) + 222/54 = 3 целых 51/54