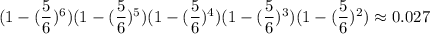7. Во всех ячейках доски размером 5×5 сидят жуки. Они одновременно все перемещаются в соседнюю ячейку в горизонтальном или вертикальном направлении. Сколько свободных ячеек может остаться в данном случае? 8. Художник раскрашивал ячейки доски размером 8×8, следуя следующему правилу: каждая следующая раскрашиваемая ячейка должна иметь только одну общую грань с другой раскрашиваемой ячейкой. Художник нарисовал 36 ячеек. Сколько ячеек вы бы покрасили больше всего?
9. Для вычерчивания всех ячеек доски размером 8×8 сколько минимум отрезков нужно прочертить.
18. Каждый квадрат и равнобедренный треугольник дополнены одинаковыми n кругами (соседние круги соединены между собой). Сколько кругов соприкасаются со всех сторон квадрата, если внутри треугольника находится 625 кругов?
19. Средний рост игроков баскетбольной команды составляет 2,04 метра. После смены игрока ростом 2,04 метра, средний рост команды составил 2,08 метра. Какова длина роста нового игрока?

👇

Открыть все ответы

Ответ:

Nikikiki303

12.12.2020

Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков

Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда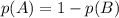 p(A)=1-p(B)

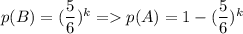Вероятность не угадать число на одном кубике равна $\dfrac{5}{6}$ (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна $p(B)=(\dfrac{5}{6})^k=p(A)=1-(\dfrac{5}{6})^k$ - это и есть искомая вероятность в данной задаче.

Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна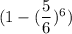 $(1-(\dfrac{5}{6})^6)$ . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 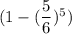$(1-(\dfrac{5}{6})^5)$ . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна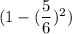 $(1-(\dfrac{5}{6})^2)$

Тогда искомая вероятность $(1-(\dfrac{5}{6})^6)(1-(\dfrac{5}{6})^5)(1-(\dfrac{5}{6})^4)(1-(\dfrac{5}{6})^3)(1-(\dfrac{5}{6})^2)\approx 0.027$

4,7(83 оценок)

Ответ:

edinorogsasha

12.12.2020

1.Решите уравнение:
1)
x + 12 = 7;
x=7-12
x=-5

2)
−13 − x = 7;
x=-13-7
x=-20

3)
3,2 − x = 8;
x=3,2-8
x=-4,8

4)
−0,4x = 8.
x=8:(-0,4)
x=-20

2.Решите уравнение:
1)
6x − 8 = 4x;
6x-4x=8
2x=8
x=8:2
x=4

2)
2х + 3 = x − 5;
2x-x=-5-3
x=-8

3)
3( 6x + 3) = 12x − 3.
18x+9=12x-3
18x-12x=-3-9
6x=-12
x=-12:6
x=-2

3.На двух полках 36 кг книг, причем на одной из них в 3 раза больше чем на другой. Сколько книг было на каждой полке?

3+1=4части
36:4=9книг на одной полке
9*3=27книг на другой полке

4. Три брата собрали 88 кг яблок. Старший собрал в 3 раза больше, чем младший, а средний — на 13 кг больше, чем младший. Сколько килограммов яблок собрал младший брат?

x -собрал младший
3x -собрал старший
x+13 -собрал средний
88кг всего
x+3x+x+13=88
5x+13=88
5x=88-13
5x=75
x=75:5
x=15кг собрал младший

5. Решите уравнение:
1)
17x − 8 = 20x + 7.;
20x-17x=-8-7
3x=-15
x=-15:3
x=-5

2)
8x − 3(2x + 1) = 2x + 4 ;
8x-6x-3=2x+4
2x-3=2x+4
2x-2x=4+3
0 не равно 7
уравнение не имеет корней

3)
0,6(x − 2) + 4,6 = 0,4(7 + x);
0,6x-1,2+4,6=2,8+0,4x
0,6x+3,4=2,8+0,4x
0,6x-0,4x=2,8-3,4
0,2x=-0,6
x=-0,6:0,2
x=-3

6. В двух цистернах было поровну воды. Когда из первой цистерны взяли 54 л воды, а из второй — 6 л, то в первой цистерне осталось в 4 раза меньше воды, чем во второй. Сколько литров воды было в каждой цистерне вначале?

x -в каждой цистерне
x-54 -осталось в первой цистерне
x-6 -осталось во второй цистерне
но известно что в первой в 4раза осталось меньше
составим уравнение

4(x-54)=x-6
4x-216=x-6
4x-x=-6+216
3x=210
x=210:3
x=70литров воды было в каждой цистерне

7. Решите уравнение
(3x + 42)(4,8 − 0,6x) = 0

3x+42=0 4,8-0,6x=0
3x=-42 0,6x=4,8
x=-42:3 x=4,8:0,6
x=-14 x=8

ответ: -14 ; 8.

4,7(25 оценок)

Это интересно:

Компьютеры-и-электроника

04.11.2021

Как создавать QR‐коды с помощью Android...

Компьютеры-и-электроника

12.03.2021

Как подготовить кабель Ethernet и объединить два ноутбука в сеть...

Путешествия

23.11.2022

Как безопасно путешествовать по Южной Африке...

Компьютеры-и-электроника