Пошаговое объяснение:
Такую систему можно решить либо таким либо матричным методом. Т.е.
A*X=B
Где A- матрица 3 на 3, где ее элементами являются коэффициенты
X- матрица 3 на 1(в столбик x1, x2, x3)
А В-матрица 3 на 1(в столбик 0, 0, 0)
Решается это уравнение так:
Х=А^-1 *В
А^-1 - это обратная матрица А
Теперь разберу с листочка:
1.Первым делом мы выписываем матрицу А
2.Далее находим ее определитель. В нашем случае равен 29(ну возможно, я где-то обсчиталась, но здесь роли не играет)
3. Первый столбец отвечает за х1, второй - за х2, ну с х3 аналогично. (если хочешь объяснение математическое, то это лучше к учебникам. Я объясняю простым языком, чтобы запоминалось)
Поочерёдно замещаем каждый столбец на матрицу В(0,0,0 в столбик) и считаем определители
Далее есть такая хрень, что определитель матрицы с замененным столбом n, деленный на определитель исходной матрицы = численному значению х n-ое
Т. Е. У нас
det х1/ detА= 0/29=0
det х2/ detА= 0/29=0
Ну можно посчитать и х3 также. Но иногда бывает удобнее подставить в какое-нибудь уравнение, как показала я. И х3 тоже =0

Пошаговое объяснение:
Система
x-9x₂=83
5x-5x₁+2x₂=50
2x₁+3x₂=6
Система
x=83+9x₂
5x-5x₁+2x₂=50
2x₁+3x₂=6
(подставляем значение X «x=83+9x₂» в «5x-5x₁+2x₂=50»)
Система
5(83+9x₂)-5x₁+2x₂=50 (раскрываем скобки и считаем это и сами сможете)
2x₁+3x₂=6
Система(итог) (теперь обе части уравнения умножаем на 2 и на 5 соответственно)
-5x₁+47x₂=-365
2x₁+3x₂=6
Система (исключаем одну из переменных путём сложения уравнений)
-10x₁+94x₂=-730
10x₁+15x₂=30
получим
109x₂=-700
x₂= -700/109
теперь данный x₂
подставляем в 2x₁+3x₂=6
получаем
2x₁+3(-700/109)=6
решаем относительно
x₁ получаем что
x₁= 1377/109
подставим это в x=83+9x₂
получим
x=83+9(1377/109)
упрощаем получается
x=2747/109
и того x,x₁,x₂ (см рис)
можно проверить подставить любой из x во все уравнения но это сами справитесь
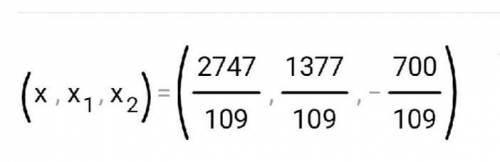
A=kN+a
B=sN+b
kN+sN делится на N нацело
Тогда остаток от деления на сумму равен:
a+b если a+b <N
a+b-N если a+b >= N (остаток всегда меньше делителя)
kN-sN делится на N нацело
Тогда остаток от деления на разность равен:
a-b если a-b > 0
N-(a-b) если a-b <=0
(kN+a)(sN+b)
kNb+sNa+ksN^2 делится нацело
Остаток равен ab если ab<N
Остаток равен остатку от деления ab на N(невозможно записать проще)
A/B=(kN+a)/(sN+b)
Воспользуемся сравнениями по модулям
A==a(mod N)
B==b(modN)
A/B==a/b(mod N)
Тогда остаток будет = a/b, но мы сможем его найти только если остатки a и b делятся друг на друга нацело и A/B тоже делятся друг на друга нацело.