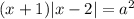
Первый аналитический)
1) Если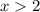 
, то 
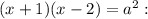
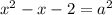
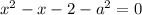
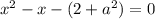
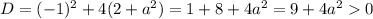
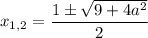
Проверим условие 
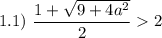
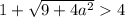
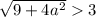
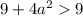
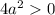
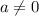
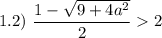
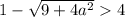
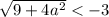
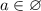
Таким образом, если 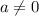, то имеем корень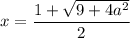 
2) Если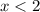 
, то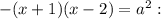 
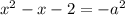
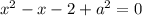
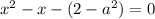
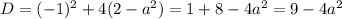
Найдем такие значения 
, при которых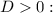 
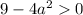
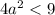
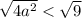
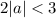
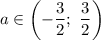
Тогда корни:
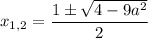
Проверим условие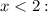 
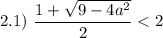
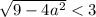
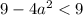
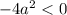
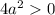
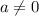
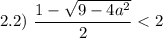
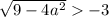
![a \in \left[-\dfrac{3}{2}; \ \dfrac{3}{2} \right]](/tpl/images/1359/4428/7966b.png)
С учетом 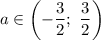имеем: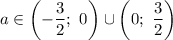 
Таким образом, при 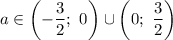имеем три корня.
Второй графический)
Рассмотрим две функции:
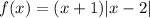
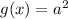— линейная функция, график — прямая, параллельная оси абсцисс
Изобразим на координатной плоскости функцию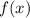 
1) Если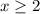 
, то 
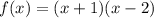— квадратичная функция, график — парабола, ветви параболы направлены вверх
2) Если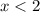 
, то 
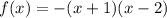— квадратичная функция, график — парабола, ветви параболы направлены вниз
Вершина параболы: 
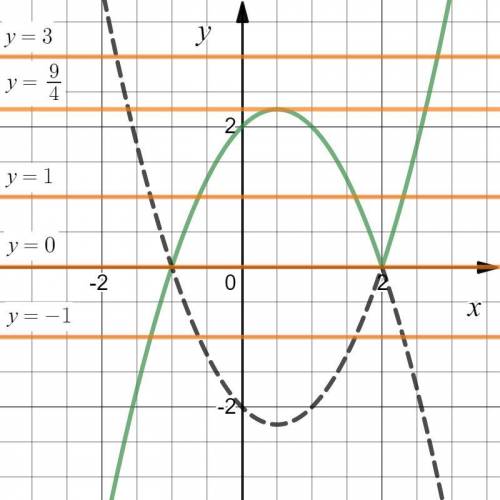
Изобразим данные функции на соответствующих участках (см. вложение).
Уравнение 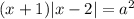будет иметь три корня, если будет три пересечения графика функции 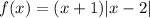c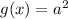
Так будет, ес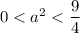ли 
или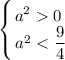 
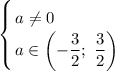
Решением системы будет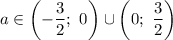
Таким образом, при 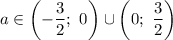имеем три корня.
ответ: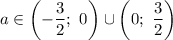
хотите проникнуться зимним спокойствием и умиротворением? - простое с однородными членами
разглядывайте морозные узоры на оконном стекле, вглядывайтесь в их красоту! - простое с однородными членами
к сожалению, во многих современных квартирах, оборудованных модными стеклопакетами, невозможно наслаждаться фантастическими узорами, которые рисует мороз. - сложноподчиненное, две основы:
1. невозможно наслаждаться
2. рисует мороз
и все же вглядитесь! - простое
вот крепкий утренний морозец инеем обметал молодой ледок на речке, а кое -где, даже разбросал гирлянды цветов. простое с однородными членами
крупные лепестки выведены рельефно и ажурно. простое с однородными членами