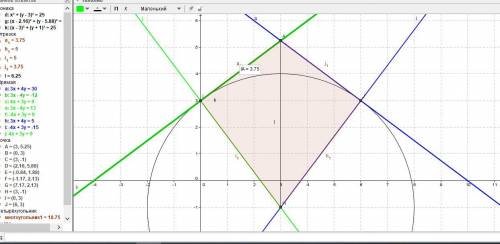
Даны прямые 3х +4y — 30 = 0, 3х – 4y +12 = 0 и окружность радиуса R = 5.
Находим точку пересечения прямых как вершину заданного четырёхугольника.
3х +4y — 30 = 0,
3х – 4y +12 = 0, сложим уравнения.
6х — 18 = 0, х = 18/6 = 3. у = (3х + 12\4 = (3*3 + 12)/4 = 21/4 = 5,25.
Точка А(3; (21/4)).
Находим угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, который вычисляется по формуле:
cos φ = (A1A2 + B1B2)/(√(A1² + B1²)*√(A2² + B2²)).
По формуле находим:
cos φ = (3*3 + 4*(-4)/(√(3² + 4²)*√(3² + (-4)²) = -7/25.
cos φ = -7/25 = -0,28.
φ = arccos(-0,28) = 1,85459 радиан или 106,2602 градуса.
Отрезок, соединяющий вершину А и центр окружности как биссектриса делит этот угол пополам.
Найдём его тангенс.
tg(φ/2) = √((1 - cos φ)/(1 + φ)) = √((1 - (-7/25))/(1 + (-7/25)) = √(32/18) = 4/3.
Теперь можно найти сторону "а" четырёхугольника.
а = R/tg(φ/2) = 5/(4/3) = 15/4 = 3,75.
Площадь четырёхугольника равна площади двух равных прямоугольных треугольников.
S = 2*((1/2)*5*(15/4)) = 75/4 = 18,75 кв.ед.
1) Б. купит все три товара сразу - не имеет смысла, заплатит 6900 руб., а участником акции не станет.
2) Б. купит сначала куртку и рубашку, а потом перчатки со скидкой - в этом случае он заплатит 4500+800=5300 руб. за куртку и рубашку, а за третью вещь, с учетом скидки заплатит 1600 - 1600*0,1 = 1440 руб., таким образо вся покупка ему обойдется в 5300+1440=6740 руб.
3) Б. купит сначала куртку и перчатки, а потом рубашку со скидкой - этот вариант тоже дает возможность участвовать в акции, но т.к. цена рубашки меньше, то и скидка будет меньше.
ответ: Б. заплатит за покупку 6740 руб.
Произведение взаимно обратных чисел равно единице (правило).
1,6 · 0,625 = 1
Следовательно, числа 1,6 и 0,625 взаимно обратные
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
2 6/17 = (2·17+6)/17 = 40/17
0,425 = 425/1000 = (425:25)/(1000:25) = 17/40 - сократили на 25
2 6/17 · 0,425 = 40/17 · 17/40 = (1·1)/(1·1) = 1/1 = 1
Следовательно, числа 2 6/17 и 0,425 взаимно обратные