Группа «65 дней помех» разработала специальное круговое пианино, где играющий стоит внутри кольца, образованного клавишами. Их пианино имеет 41 клавишу. Фронтмен группы начинает играть мелодию: он нажимает на клавишу, отступает на одну клавишу налево от нажатой и жмёт, затем отступает ещё на две клавиши налево и жмёт, затем отступает дальше на три клавиши налево и жмёт (то есть, в четвёртый раз фронтмен нажал шестую клавишу от той клавиши, которая была нажата первой). На каком по счёту нажатии фронтмен нажмёт на клавишу, с которой начинал?

👇

Увидеть ответ

Ответ:

данил20888

01.05.2023

Пошаговое объяснение:

По кароче напиши

4,4(10 оценок)

Открыть все ответы

Ответ:

Vladamira55

01.05.2023

Последовательности удовлетворяющие условию будем называть "правильными". Любая правильная последовательность начинается с +1 (по условию) и заканчивается на -1 (иначе $a_1+a_2+\ldots+a_{2n-1}< 0$ ).

Правильную последовательность длины 2n можно получить так:
1) Выбрать произвольное k с условием 0≤k≤n-1.
2) Между 1 и -1 вставить любую правильную последовательность длиной 2k.
3) К полученной последовательности приписать правильную последовательность длиной 2(n-k-1). При этом, если надо приписывать или вставлять последовательность нулевой длины, то ничего не делаем.
В итоге, получается последовательность длиной 2+2k+2(n-k-1)=2n. Причем, эта последовательность обязательно правильная, т.к.
a) $a_1+a_2+\ldots+a_{j}\ge 1$ при 1≤j≤2k+1 (т.к. после начальной 1 мы приписали правильную длиной 2k)
б) $a_1+a_2+\ldots+a_{j}= 0$ при j=2k+2 (т.к. сумма всех элементов правильной равно 0 и сумма 1 и -1 тоже 0)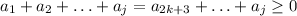
в) $a_1+a_2+\ldots+a_{j}=a_{2k+3}+\ldots+a_{j}\ge 0$ при 2k+3≤j≤2n (при k=n-1 этой части нет).
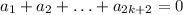Обратное тоже верно. Любую правильную последовательность длины 2n можно представить в таком виде. Действительно, в качестве k можно выбрать первое такое k, что $a_1+a_2+\ldots+a_{2k+2}= 0$ . Тогда a_1=1

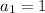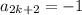, $a_{2k+2}=-1$ , а все последовательные суммы элементов между ними больше или равны 0, т.к. все суммы начиная с первой единицы больше или равны 1 (не забываем, что мы выбрали ПЕРВОЕ такое k). Т.е. между 1 и -1 находится правильная последовательность длины 2k. Все, что находится после этих 2k+2 элементов, очевидно, также является правильной последовательностью.Таким образом, для произвольной правильной последовательности длины 2n выполнены все условия а), б), в).

Из этого построения следует рекуррентная формула для числа всех правильных последовательностей длины 2n. Обозначим через c_k

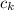число правильынх последовательностей длины 2k. Тогда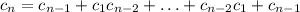
$c_{n}=c_{n-1}+c_1c_{n-2}+\ldots+c_{n-2}c_1+c_{n-1}$
Здесь первое слагаемое соответствует k=0, т.е.это количество всех правильных последовательностей вида {1,-1, произвольная правильная последовательность длины 2(n-1)}.
Второе слагаемое соответствует k=1, когда последовательности имеют вид
{1, все правильные последовательности длины 2, -1, все правильные последовательности длины 2(n-2)}. И т.д.
Итак, для n=7:
c_1=1

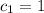(такая последовательность всего одна: {1,-1})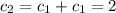
c_2=c_1+c_1=2

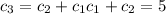
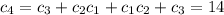
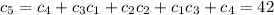
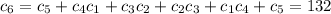
c_6=c_5+c_4c_1+c_3c_2+c_2c_3+c_1c_4+c_5=132

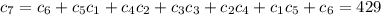
c_7=c_6+c_5c_1+c_4c_2+c_3c_3+c_2c_4+c_1c_5+c_6=429

ответ: 429.

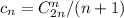P.S. Полученное рекуррентное соотношение можно упростить, и доказать, что $c_n=C_{2n}^n/(n+1)$ . Это можно доказать по индукции, или с производящих функций. Сама задача эквивалентна задаче о количестве правильных расстановок 2n скобок (n открывающих и n закрывающих). Открывающая скобка соответствует +1, и закрывающая соответствует -1. (число открывающих скобок левее k-oй позиции не меньше числа закрывающих). Количество таких расстановок называется числом Каталана. Есть еще множество интересных переформулировок этой задачи. Все можно найти в интернете по запросу "Числа Каталана".