1)было-8 кг
продали-5 кг
осталось-?
8-5=3 кг
2)было-?
продали-7
осталось 9
9+7=16 кг было
Пошаговое объяснение:
Игорь Грабарь - известный русский художник-пейзажист. Наверное, многие видели его замечательные картины, такие как "На озере", "Сентябрьский снег" или "Зимний пейзаж". "Февральская лазурь" - одно из самых завораживающих его произведений. Но ало кто знает, что эта картина была написана случайно. Художник просто нагнулся что-то поднять и увидел фантастической красоты пейзаж. Ослепляющее своей голубизной небо, белоствольная красавица-берёза и чуть сиреневатый снег поразили Грабаря. И он, окрылённый вдохновением, написал картину "Февральская лазурь".
Зимние пейзажи всегда очень красивы. Настолько, что хочется смотреть на них вечно, так же и на картину Грабаря. На полотне он изобразил поразительной красоты момент. Небо такое ярко-синее и бездонное сверху, а не горизонте светло-голубое, чистое. Плавный переход в цветах оживляет его, оно становится более объёмным. Снег словно искрится, он окрашен во множество разных оттенков. На солнце он нежный, беловато-розового цвета, а в тени зеленовато-голубой, чем то похожий на небо. На переднем плане изображена слегка изогнутая берёзка, которая раскинула свои ветви, словно в непонятном, но очень красивом танце. Художник очень живо изобразил русскую красавицу, и иногда кажется, что она стоит прямо перед нами. На её ветви мягко опускается пушистый снежный покров, а на земле лежат глубокие сугробы, что кажется, как будто ты сейчас провалишься.
На заднем плане мы видим целую берёзовую рощу. Деревья, словно наблюдают за неким спектаклем, в котором играет наша красавица и её друзья-соседи.
Белая берёзка - символ русских лесов, лазоревое небо и сиреневато-голубой снег. Всё так и дышит приятной морозной свежестью. Мне очень нравится картина "Февральская лазурь" своей живостью, такой, что она больше похожа на фотографию. Художник отлично предал радостное настроение февральского дня. Он нарисовал всё в такой сине-голубой гамме, в какой только можно передать дыхание зимы.
Мне кажется, что вот-вот и я окажусь там, среди белых берёзок и буду вдыхать тот чистый, прохладный воздух.
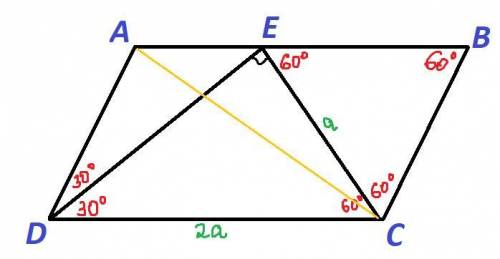
Так как угол ADC равен π/3, то есть 60°, и DE - биссектриса угла ADC, то углы ADE и CDE равны по 60°:2=30°.
Сумма смежных углов параллелограмма равна 180°, значит:
∠BCD=180°-∠ADC=180°-60°=120°
Так как угол BCD равен 120° и CE - биссектриса угла BCD, то углы BCE и DCE равны по 120°:2=60°.
Рассмотрим треугольник CDE. Так как два угла в нем известны, то найдем третий угол CED:
∠CED=180°-∠CDE-∠DCE=180°-30°-60°=90°
Значит, треугольник CDE - прямоугольный.
В прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы.
Введем обозначения. Пусть катет CE, лежащий против угла в 30°, равен a. Тогда гипотенуза CD равна 2а. Заметим, что CD соответствует одной из сторон параллелограмма.
Рассмотрим треугольник ВСЕ. Найдем неизвестные его углы.
Так как противоположные углы параллелограмма равны, то:
∠ABC=∠ADC=60°
Зная два угла треугольника, найдем третий:
∠BEC=180°-∠BCE-∠CBE=180°-60°-60°=60°
Все углы треугольника ВСЕ равны, значит он - равносторонний.
Одна из сторон треугольника ВСЕ обозначена как а, значит и все его стороны равны а. В том числе, сторона параллелограмма ВС=а.
Таким образом, известны в наших обозначениях стороны параллелограмма: AB=DC=2a, BC=AD=a.
Рассмотрим треугольник АВС. Запишем для него теорему косинусов:
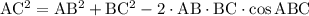
Подставим известные соотношения:
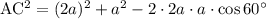
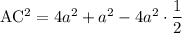
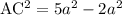
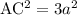
По условию АС=3.
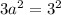
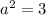
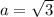(отрицательный корень смысла не имеет)
Вернемся к треугольнику CDE. Две стороны в нем теперь известны: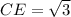 
, 
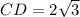. Запишем теорему Пифагора:
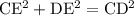
Выражаем искомый отрезок DE:
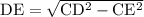
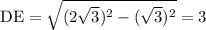
ответ: 3
1)в магазине продали 7 кг конфет.после этого осталось 9 кг конфет.Сколько всего было конфет в магазине?
7+9=16(кг)-конфет всего было в магазине
2)в первый день в магазин привезли 5 кг печенья ,а во второй день привезли 8 кг печенья.На следующие дни продали 7 кг печенья.Сколько кг печенья осталось?
1)5+8=13(кг)-привезли за 2 дня
2)13-7=6(кг)-печенья осталось