Немного не то, смотрите: когда у нас просят вычислить площадь фигуры (или же трапеции), ограниченной линиями, тогда мы должны использовать формулу Ньютона-Лейбница: - простыми словами, находим интегралы линии, которой ограничена трапеция, a и b - на каком отрезке расположена трапеция.
Сперва в задаче нужно нарисовать графики и прямые на числовой прямой, что указаны в условии: , , , . Примерный график прикрепляю.
Глядя на рисунок, можем сказать, что расположен над осью ОХ, значит можем найти площадь таким образом: см²
Во время путешествий колобок попал в страну геометрических фигур. Он видел там много ученых, которые их чертят, у них были очень большие линейки. По улицам ходили квадраты треугольники прямоугольники и много других геометр фигур. Пообщавшись с квадратом, колобок узнал, что царицей их города была прекрасная принцесса Шестиугольник. Никто из города не знал ее периметра. Колобок отправился к ней и спросил ее периметр, на что Шестиугольник ответила, что одна ее сторона равна 3см. Все стороны у шестиугольников равны. 6*3=18.
Відповідь:
Покрокове пояснення:
Немного не то, смотрите: когда у нас просят вычислить площадь фигуры (или же трапеции), ограниченной линиями, тогда мы должны использовать формулу Ньютона-Лейбница:
- простыми словами, находим интегралы линии, которой ограничена трапеция, a и b - на каком отрезке расположена трапеция.
Сперва в задаче нужно нарисовать графики и прямые на числовой прямой, что указаны в условии:
, 
, 
, 
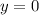. Примерный график прикрепляю.
Глядя на рисунок, можем сказать, что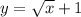
расположен над осью ОХ, значит можем найти площадь таким образом: 
см²