Дано: y1 = 1/3*x², y1 = 4 - 2/3*x²
Найти площадь фигуры.
Пошаговое объяснение:
Площадь - интеграл разности функций.
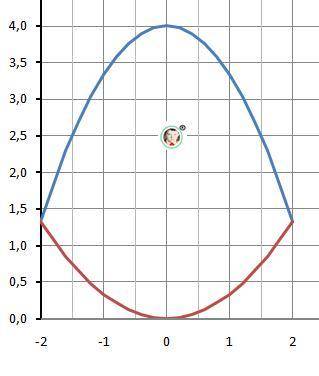
Рисунок к задаче в приложении.
График функции у1 - выше, чем у функции у2.
Находим точки пересечения - решаем квадратное уравнение разности функций.
- 2/3*x² + 4 = 1/3*x²
-x² + 4 = (2-x)*(2+x) = 0
b = 2 - верхний предел, a = - 2 - нижний предел.
Находим интеграл разности функций - пишем в обратном порядке.
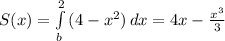
Вычисляем
S(2)= 8 - 2 2/3 = 5 1/3
S(-2) = -8 + 2 2/3 = - 5 1/3
S = S(2) - S(-2) = 10 2/3 - площадь - ответ.
Рисунок к задаче в приложении.
Пошаговое объяснение:
ДАНО:Y(x) = 2*x³ -3*x² -12*x +21
ИССЛЕДОВАНИЕ.
1. Область определения D(y) ∈ R, Х∈(-∞;+∞) - непрерывная , гладкая.
2. Первая производная. Y'(x) = 6*x² -6*x -12 = 0
Корни Y'(x)=0. Х = -1 Х = 2
Производная отрицательна между корнями - функция убывает.
3. Локальные экстремумы.
Максимум - Ymax(-1) = 28. Минимум - Ymin(2) = 1 - ответ.
Дополнительно.
4. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;-1;]U[2;+∞) , убывает - Х∈[-1;2]
5. Вторая производная - Y"(x) = 12* x -6 = 0
Корень производной - точка перегиба Х₆=0,5
6. Выпуклая “горка» Х∈(-∞; Х₆ = 0,5]
Вогнутая – «ложка» Х∈[Х₆ = 0,5; +∞).
7. График в приложении.

Пошаговое объяснение:
21÷8=2 с ост.5 проверка:8×2=16+5=21
19÷3=6 с ост.1 проверка:3×6=18+1=19
37÷9=4 с ост.1 проверка:9×4=36+1=37
21÷4=5 с ост.1 проверка:5×4=20+1=21
39÷5=7 с ост.4 проверка:5×7=35+4=39
45÷6=7 с ост.3 проверка:6×7=42+3=45
15÷6=2 с ост.3 проверка: 6×2=12+3=15
50÷7=7 с ост.1 проверка:7×7=49+1=50
67÷8=8 с ост.3 проверка:8×8=64+3=67
75÷9=8 ост.3 проверка:9×8=72+3=75
28÷6=4 ост.4 проверка:6×4=24+4=28
26÷3=8 ост.2 проверка:3×8=24+2=26
:)