Пошаговое объяснение:
1) общий знаменатель 100 делим на 25 получается 4 и умножаем на 44 и получается, так же проделываем и со второй дробью: 11/25 - 7/20 = 44/100-35/100=9/100
2) общий знаменатель 168 делим на 35 получается 4 и умножаем на 35 и получается 140/168, так же проделываем и со второй дробью: 140/168-119/168=21/168
3) общий знаменатель 48 делим на 24 получается 2 и умножаем на 11 и получается 22/48, так же проделываем и со второй дробью: 22/48+9/48=31/48
4) общий знаменатель 45 делим на 5 получается 9 и умножаем на 2 и получается 18/45, так же проделываем и со второй дробью и с третьей дробью и получается: 18/45+12/45-10/45=20/45, эту дробь сокращаем на 5,получается 4/9.
5) В этом примере переводим в обыкновенную дробь, т.е. 5*16+3=83/16, первую дробь не трогаем так как она у нас уже приведена к общему знаменателю, общий знаменатель 16 делим на 8 получается 2 и умножаем на 5 и получается 10/16, 83/16-10/16=73/16, выделяем целую часть получается 4 целых 9/16

1 , –1 , 2 .
Пошаговое объяснение:
А) по формулам Крамера:
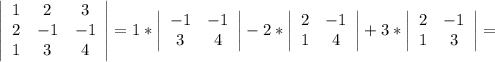
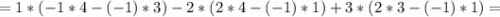
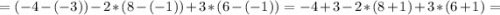
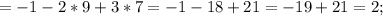
Определитель не равен нулю ⇒ матрица совместна.
Теперь поочерёдно вместо 1-го, 2-го и 3-го столбцов будем подставлять столбец свободных членов:
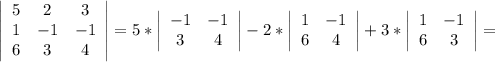
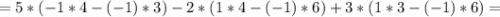
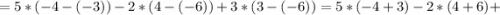
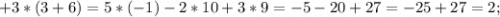
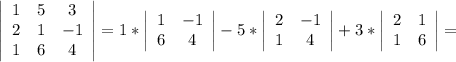
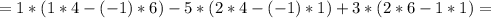
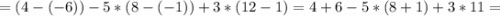
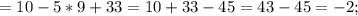
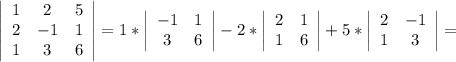
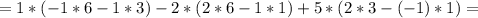
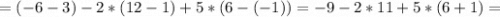
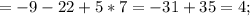
Для того, чтобы найти x, y и z, разделим значения полученных определителей на значение исходного определителя соответственно:
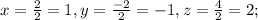
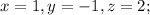
Б) методом Гаусса:
Запишем матрицу, элементами которой являются коэффициенты при переменных. За чертой расположим свободные члены:
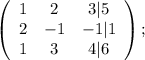
Умножая все элементы первой строки на –2 и складывая почленно с элементами второй строки, получим:
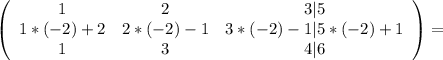
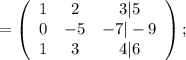
Умножая все элементы первой строки на –1 и складывая почленно с элементами третьей строки, получим:
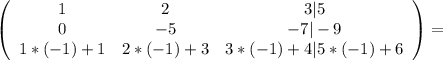
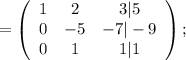
Умножая все элементы второй строки на 0,2 и складывая почленно с элементами третьей строки, получим:
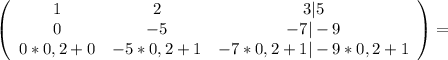
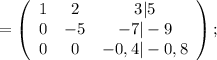
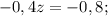
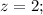
Запишем систему уравнений с новыми данными:
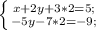
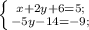
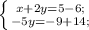
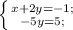
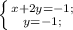
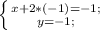
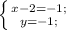
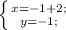
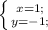
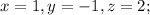
-(-3)-(-1)-(1)(2)--(5)
Пошаговое объяснение:
в скобочках числа, где дефисы пустая ось