За 30 1. признаки делимости на 5 и на 2. пример. 2. признаки делимости на 10 и на 2. пример. 3. признаки делимости на 9 и на 3. пример. 4. какие числа называют простыми? пример. 5. какие числа называют составными? пример. 6. что называют наибольшим общим делителем? пример. 7. как найти нод? пример. 8. что называют наименьшим общим кратным? пример. 9. как найти нок? пример. 10. основное свойство дроби. пример. 11. как дроби к общему знаменателю? опишите последовательность действий. 12. что нужно сделать, чтобы сложить дроби с разными знаменателями? пример. 13. что нужно сделать, чтобы сравнить дроби с разными знаменателями? пример. 14. как умножить число на дробь? пример. 15. как умножить дробь на дробь? пример. 16. какие числа называют смешанными? пример. 17. как найти дробь от числа? пример. 18. какие числа называют взаимно обратными? пример. 19. какие числа называют взаимно простыми? пример. 20. как разделить дробь на дробь? пример. 21. как найти число по его дроби? пример. 22. что называют пропорцией? пример. 23. основное свойство пропорции. пример. 24. какая пропорциональная зависимость называется прямой? пример. 25. какая пропорциональная зависимость называется обратной? пример. 26. что называют масштабом? 27. формулы длины окружности и площади круга. 28. положительные и отрицательные числа. изображение на координатной прямой. 29. целые числа. рациональные числа. пример. 30. модуль числа. 31. сложение и вычитание рациональных чисел. правила сложения. пример. 32. умножение и деление рациональных чисел. правила сложения. пример. 33. коэффициент. пример. 34. распределительное свойство умножения относительно сложения и вычитания. подобных слагаемых. пример. 35. параллельные прямые. определение и чертеж. 36. перпендикулярные прямые. определение. чертеж. 37. координатная плоскость. пример построения координатной плоскости и нескольких точек с произвольными координатами. 38. графики. пример построения графика, заданного формулой у=2х.
 задач
задач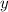 задач
задач задач
задач 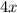 задач
задач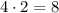 задач.
задач.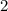 задачи
задачи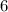 задач
задач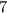 задач
задач 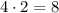 задач
задач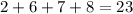 задачи
задачи
199 чисел кратны 5 : [999 : 5] = 199 .
В этом же интервале имеются 142 числа, кратных 7 : [999 : 7] = 142 .
Среди 142 чисел, кратных 7, имеются числа, которые делятся также и на 5, то есть кратные 35.
Всего таких чисел 28: [999 : 35]= 28
Эти 28 чисел уже учтены в числе 199, найденном ранее.
Поэтому количество чисел, меньших 1000, которые делятся либо на 5, либо на 7, равно 199 + 142 - 28 = 313.
В рассматриваемом интервале остается 999 - 313 = 686 чисел,
которые не делятся ни на 5, ни на 7
* [N] - целая часть числа N . Например, [13,45] = 13.
точно не знаю правильно ли это,но вроде бы равильно