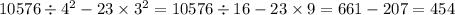
|AB|=√((0-(-4))^2+(-1-2)^2=√16+9=√25=5
уравнение AB:
x+4/4=y-2/-3
-3(x+4)=4(y-2)
-3x-12=4y-8
3x+12+4y-8=0
3x+4y+4=0
BC:
x/3=y+1/4
4x=3(y+1)
4x=3y+3
4x-3y-3=0
AC:
x+4/7=y-2/1
x+4=7y-14
x-7y+4+14=0
x-7y+18=0
Внутренний угол при вершине A:
AB(4;-3)
AC(7;1)
|AC|=√49+1=√50=5√2
cos(AB^AC)=28-3/5*5√2=25/25√2=1/√2=45 градусов
Чтобы найти уравнение высоты, проведенный через вершину С, надо найти середину отрезка AB. Высоту обозначим CH.
Отсюда видим,что H - середина отрезка AB:
xh=-4+2/2=-2/2=-1
yh=2-1/2=1/2=0.5
⇒H(-1;0.5)
Находим уравнение высоты CH:
C(3;3)
H(-1;0.5)
x-3/-1-3=y-3/0.5-3
x-3/-4=y-3/-2.5
-2.5(x-3)=-4(y-3)
-2.5x+7.5=-4y+12
2.5x+4y+12-7.5=0
2.5x+4y+4.5=0
Для медианы находим середину отрезка AC:
Медиана BM:
xm=-4+3/2=-1/2=-0.5
ym=2+3/2=5/2=2.5
⇒M(-0.5;2.5)
B(0;-1)
Находим уравнение медианы BM:
x+0.5/0.5=y-2.5/-3.5
-3.5(x+0.5)=0.5(y-2.5)
-3.5x-1.75=0.5y-12.5
3.5x+0.5y+1.75-12.5=0
3.5x+0.5y-10.75=0
Чтобы найти точку пересечения высот надо найти либо середину медианы BM, либо середину высоты CH:
Я найду середину CH:
C(3;3)
H(-1;0.5)
Пусть точка N(xn;yn) - середина CH, тогда:
xn=3-1/2=2/2=1
yn=3+0.5/2=3.5/2=1.75
N(1;1.75)
S=1/2AB*AC
S=5*5√2/2=25/2/2=12.5√2 ед^2
Пошаговое объяснение: