1) -3
2) 0
3) ∞
Пошаговое объяснение:
Для вычисления предела на бесконечности частного двух многочленов можно сравнить степени многочленов - если степень числителя больше, то предел частного будет равен бесконечности. если степени одинаковые, то предел будет равен отношению коэффициентов при старших степенях. Если степень в значменателе больше, то предел будет равен нулю. Примеры на все три случая:
1) 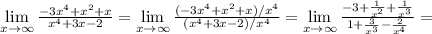
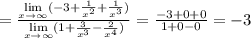
2) 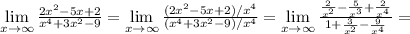
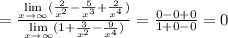
3)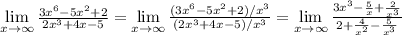
В числителе стоит бесконечно большая функция, знаменатель стремится к 2 (то есть имеет конечный предел), значит частное будет бесконечно большим.
Длины сторон параллелограмма:
АВ = CD = 3 см; ВС = AD = 9 см
Пошаговое объяснение:
Требуется найти стороны параллелограмма.
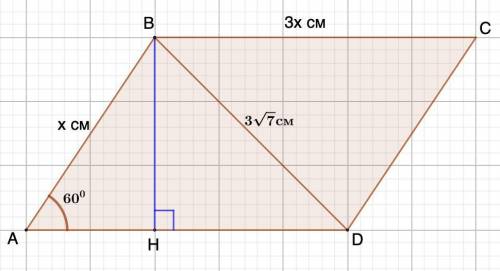
Для того, чтобы решить задачу, сделаем чертеж.
Из вершины В опустим высоту на AD.
Дано: ABCD - параллелограмм;
ВС : АВ = 3;
BD = 3√7 см; ∠А = 60°.
Найти: AB; BC; CD; AD.
1. По условию: ВС : АВ = 3.
Пусть АВ = х см, тогда ВС = 3х см.
Противоположные стороны параллелограмма равны.⇒ АВ = CD = x см; ВС = AD = 3x см.
2. Рассмотрим ΔАВН - прямоугольный.
∠А = 60° (по условию)
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠АВН = 90° - 60° = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ 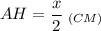
По теореме Пифагора:
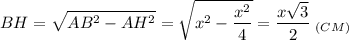
3. Рассмотрим ΔHBD - прямоугольный.
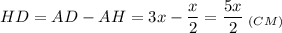
По теореме Пифагора:
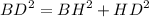
Подставим значения и решим уравнение:
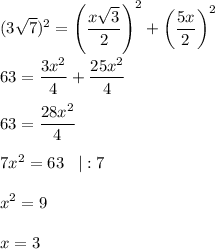
Стороны АВ = CD = 3 см.
Найдем ВС:
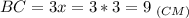
Стороны ВС = AD = 9 см.
17+8=25; 25^2=625
21-17=4; 4^3=64