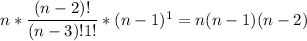Тут, очевидно, опечатка, k<n. В дереве на n вершинах не может быть вершины степени n.
n=1:
k=0 - одно дерево, состоящее из одной вершины.
n=2:
k=0 => граф не связный => не деревоk=1 => одно дерево, состоящее из одного ребра
n>2:
k=0 => граф не связный => не деревоk>0 => Тогда каждому дереву поставим в соответствие код Прюфера. Его длина - n-2. Т.к. вершина 1 имеет степень k, то встречается в нем k-1 раз. Тогда для остальных n-1 вершин остается n-2-(k-1)=n-k-1 мест. Тогда всего таких кодов Прюфера, и, следовательно, деревьев,
Задание 3
Найти количество деревьев с n вершинами, имеющими вершину степени n-2.
Зафиксируем номер этой вершины. Тогда в коде Прюфера она встречается n-3 раз. Тогда для остальных n-1 вершин остается n-2-(n-3)=1 место. Кол-во выбора номера вершины степени n-2 из n равно n. Тогда искомое число деревьев равно
1) я думаю, что особенность портрета и музыки Моцарта заключается в том, что Моцарт написал около 41 симфонии, но в период написания ранних симфоний ещё не сформировалась его индивидуальность, стиль композиции. В ней собраны все достижения Моцарта в плане композиции. Симфония №40 отличается единством образов и эмоций, особенно в 1й части, которая как раз более всего популярна. В симфонии нет вступления. Она начинается с проведения главной темы, очень мелодичной, трепетной и лиричной, основанной на интонациях ламенто (нисходящие секундовые интонации) . Тема первой части яркая и запоминающаяся. Думаю, что симфония популярна именно из-за этой темы. Не думаю, что многие люди (не музыканты) знают темы 12й или 32 симфонии, но тема 40й известна практически всем. И не потому, что её "ставят в детских садах", а потому что из 41 симфонии Моцарта только последние 5 выражают всю глубину его чувств и композиторских умений.
Задание 1
ответ в приложении
Задание 2
Тут, очевидно, опечатка, k<n. В дереве на n вершинах не может быть вершины степени n.
n=1:
k=0 - одно дерево, состоящее из одной вершины.n=2:
k=0 => граф не связный => не деревоk=1 => одно дерево, состоящее из одного ребраn>2:
k=0 => граф не связный => не деревоk>0 => Тогда каждому дереву поставим в соответствие код Прюфера. Его длина - n-2. Т.к. вершина 1 имеет степень k, то встречается в нем k-1 раз. Тогда для остальных n-1 вершин остается n-2-(k-1)=n-k-1 мест. Тогда всего таких кодов Прюфера, и, следовательно, деревьев,Задание 3
Найти количество деревьев с n вершинами, имеющими вершину степени n-2.
Зафиксируем номер этой вершины. Тогда в коде Прюфера она встречается n-3 раз. Тогда для остальных n-1 вершин остается n-2-(n-3)=1 место. Кол-во выбора номера вершины степени n-2 из n равно n. Тогда искомое число деревьев равно