1) S=ab=400м*1250м=50 000 м2 = 50 га (1га =10 000м2)
2) V=abc=3м*8м*5дм=30дм*80дм*5 дм = 12 000 дм3 = 12 м3
3)
а)V=S/T=36 км / 4 ч =9км/ч
б) S=V*T=650км/ч*2ч=1300 км
в) T=S/V=40 км / 10км/ч=4 ч
5) 1) 16*4=64 см2 - площадь прямоугольника и квадрат
2) нам нужно найти такое число, которое в квадрате даст 64. это число 8, значит сторона квадрата 8 см (т.к. площадь квадрата сторону умнож. на саму себя)
6)
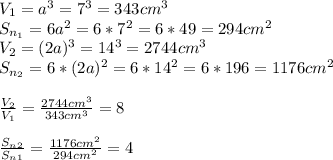
первый объем 343, второй 2744, площадь первой пов-ти 296, второй 1184, объем в 8 раз, площади в 4
7)
1) 54:6=9 см2 - площадь одной грани
2) нужно найти число, кторое в квадрате дает 9. это число 4. значит 3 - ребро куба
3) V=a^3=3^3=3*3*3=27 m3
1) проверим для n = 1:
3^(2+1) + 2*4^1 = 35 - кратно 5
2) предположим, что для n = k (k > 1) утверждение верно:
А = 3^(2k+1) + 2*4^k кратно 5
3) докажем, что оно также верно и для n = k+1:
3^(2(k+1)+1) + 2*4^(k+1) =
= 3^(2k+2+1) + 2*4^k * 4^1 =
= 3^2 * 3^(2k+1) + 8*4^k = 9 * 3^(2k+1) + 8*4^k = / выделим из этой суммы выражение А (из пункта 2) / =
= (4 * 3^(2k+1) + 8*4^k) + 5 * 3^(2k+1) =
= 4А + 5 * 3^(2k+1).
Имеем: первое слагаемое кратно 5 (см пункт 2); второе слагаемое кратно 5, так как имеет множитель 5. Следовательно, вся сумма кратна 5 => утверждение тоже верно => изначальное выражение кратно 5 при любых n из N, чтд.