ответ:Воспользуемся формулой Лапласа
вероятность, что событие наступит k раз при n испытаниях
P(k) = 1/корень (npq) * ф [ (k-np)/корень (npq) ], где
p - вероятность события, q = 1-p, ф - функция Гаусса
ф (x) = 1/корень (2pi) * e^(-x^2 / 2)
n = 1600, k = 1200, p = 0.8, q = 0.2
np = 1280, корень (npq) = 16
x = (k-np)/корень (npq) = -80 / 16 = -5
ф = 1/корень (2pi) * e^(-x^2 / 2) = 0.3989 * e^(-12.5) = 0,3989*3,731*10^(-6) = 1.488*10^(-6)
P(1200) = 1/16 * 1.488*10^(-6) = 0.93*10^(-7)
вероятность ничтожно мала - меньше одной десятимиллионной
Пошаговое объяснение:Воспользуемся формулой Лапласа
вероятность, что событие наступит k раз при n испытаниях
P(k) = 1/корень (npq) * ф [ (k-np)/корень (npq) ], где
p - вероятность события, q = 1-p, ф - функция Гаусса
ф (x) = 1/корень (2pi) * e^(-x^2 / 2)
n = 1600, k = 1200, p = 0.8, q = 0.2
np = 1280, корень (npq) = 16
x = (k-np)/корень (npq) = -80 / 16 = -5
ф = 1/корень (2pi) * e^(-x^2 / 2) = 0.3989 * e^(-12.5) = 0,3989*3,731*10^(-6) = 1.488*10^(-6)
P(1200) = 1/16 * 1.488*10^(-6) = 0.93*10^(-7)
вероятность ничтожно мала - меньше одной десятимиллионной
Привет!
Длины сторон треугольника относятся друг к другу как 6:8:10, ну или же 6х:8х:10х (1)
Найдем чему равна переменная х через периметр треугольника.
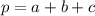
Пусть а, b, c — стороны треугольника; тогда периметр равен:
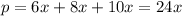
Периметр равен 24х, при этом он нам известен — 72, тогда найдем чему равен х:
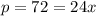
Откуда х:
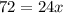
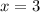
Вернемся в пункт 1, где мы приняли отношения длин сторон как 6х:8х:10х
Теперь очень легко можно найти длину каждой стороны :)
а = 6х = 6×3= 18
b = 8x = 8×3= 24
c = 10x = 10×3 = 30
ответ: стороны треугольника равны 18, 24, 30.
Удачи! :)
1) (134+34):14-х=132:22+6
168:14-х=6+6
12-х=12
х=12-12
х=0
2)240:(х-18)=226-106
240:(х-18)=120
х-18=240:120
х-18=2
х=2+18
х=20
Все