1. Предел суммы (разности) двух функций, имеющих предел, равен сумме (разности) пределов этих функций
2. Предел произведения двух функций, имеющих предел, равен произведению пределов этих функций
3. Постоянный множитель можно вынести до знака предела
4. Предел константы равен константе
5. Предел отношения двух функций, имеющих предел, равен отношению пределов этих функций
6. Для всех основных элементарных функций в любой точке их области определения имеет место
Пошаговое объяснение:
сделай как лучший ответ или хотя бы поставь лайк
Пошаговое объяснение:
здесь не будем заморачиваться тройными интегралами. посмотрим на наши поверхности
1 страшная формула - это однополостный гиперболоид
две других - это плоскости
объем тела, содержащегося между плоскостями z = а и z = Ь, выражается формулой:
 , где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.
, где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.
плоскость, перпендикулярная оси Оz, в точке с аппликатой z пересекает гиперболоид по эллипсу
запишем наш эллипс

теперь нам надо каноническое уравнение нашего эллипса
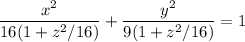
упростим

площадь этого замечательного гиперболоида вычисляется по формуле
S=πab
у нас
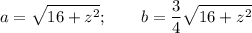
отсюда
S=π*(3/4)(16+z²)
вот, собственно, и все "загогулины"
остался только объем

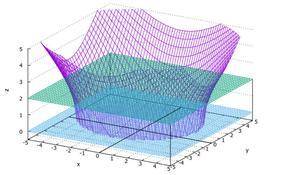
2*4=8 задача проста и легка