Вопрос 1. Одна работница обслуживает тридцать ткацких станков, обеспечивая их запуск после разрыва нити. Модель такой системы массового обслуживания можно охарактеризовать как: 1) многоканальную однофазовую с ограниченной популяцией;
2) одноканальную однофазовую с неограниченной популяцией;
3) одноканальную многофазовую с ограниченной популяцией;
4) одноканальную однофазовую с ограниченной популяцией;
5) многоканальную однофазовую с неограниченной популяцией.
Вопрос 2. В теории массового обслуживания для описания простейшего потока заявок, поступающих на вход системы, используется распределение вероятностей:
1) нормальное;
2) экспоненциальное;
3) пуассоновское;
4) биномиальное;
5) ничто из вышеуказанного не является верным.
Вопрос 3. В теории массового обслуживания предполагается, что количество заявок в популяции является:
1) фиксированным или переменным;
2) ограниченным или неограниченным;
3) известным или неизвестным;
4) случайным или детерминированным;
5) ничто из вышеуказанного не является верным.
Вопрос 4. Двумя основными параметрами, которые определяют конфигурацию системы массового обслуживания, являются:
1) темп поступления и темп обслуживания;
2) длина очереди и правило обслуживания;
3) распределение времени между заявками и распределение времени обслуживания;
4) число каналов и число фаз обслуживания;
5) ничто из вышеуказанного не является верным.
Вопрос 5. В теории массового обслуживания для описания времени, затрачиваемого на обслуживание заявок, обычно используется распределение вероятностей:
1) нормальное;
2)экспоненциальное;
3) пуассоновское;
4) биномиальное;
5) ничто из вышеуказанного не является верным.
Вопрос 6. Ремонт вышедших из строя компьютеров в институте транспорта осуществляют три специалиста, работающие одновременно и независимо друг от друга. Модель такой системы массового обслуживания можно охарактеризовать как:
1) многоканальную с ограниченной популяцией;
2) одноканальную с неограниченной популяцией;
3) одноканальную с ограниченной популяцией;
4) одноканальную с ограниченной очередью;
5) многоканальную с неограниченной популяцией.
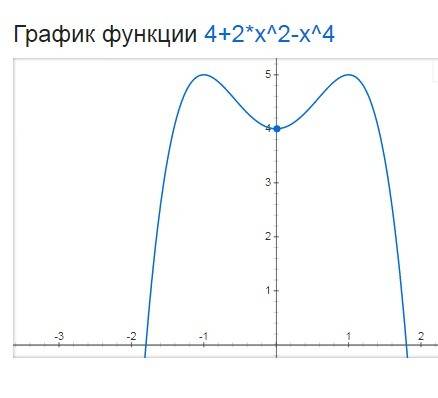
y'=0
4x(1-x²)=0
х=0 х=-1 х=1 точки экстремума
нанесем корни на числовую ось и определим знаки у' в каждом интервале
у' + - + -
---------------------------------------------------------------------------
-1 0 1
y возрастает убывает возрастает
в точках х=-1 и х=1 максимум
в точке х=0 минимум
f(-2)=4+8-16=-4
f(-1)=4+2-1=5
f(0)=4
f(1)=f(-1)=5
минимальное значение - 4
максимальное значение 5