
ответ:ответ: Р(А)=0,8
Пошаговое объяснение:1) 45-9=36 - каналов, по которым новостей нет
2) 36/45=0,8 - вероятность того, что Маша включит канал, по которым не идут новости
задание №2
Пусть событие А соответствует приезду зеленого такси к заказчице. Всего зеленых такси равно m=8, а общее число свободных такси n=20. В результате, вероятность события А, равна:
ответ: 0,4.
задание №3
4/16 = 1/4 = 0,25 (или 25%)
Нужно разделить кол-во благоприятных исходов на кол-во всех возможных вариантов.
ответ:25%
задание №4
Известно, что при бросании игрального кубика может выпасть любое целое число от 1 до 6 с вероятностью 1/6 (так как у кубика 6 граней и все они симметричны). Чтобы получилось ровно 8 очков при бросании двух игральных кубиков, возможны следующие варианты:
2+6, 3+5, 4+4, 5+3, 6+2,
то есть число благоприятных исходов m=5. Общее число возможных исходов, равно . Таким образом, искомая вероятность, равна:
ответ: 0,14.
Задание №5
На первое место претендует 20 спортсменок, то есть общее число возможных исходов, равно n=20. Среди них спортсменок из Китая ровно m=20-8-7=5 – число благоприятных исходов. Таким образом, искомая вероятность, равна:
ответ: 0,25.
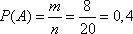


Длина средней линии треугольника равна половине длины стороны треугольника, которой параллельна эта средняя линия.
Т.к. MN || AB, то |MN|=1/2|AB|.
AB²=(1-(-1))²+(0-2)²+(4-3)²=4+4+1=9=3²
Значит, длина стороны AB равна 3, а длина средней линии MN равна 3/2=1,5.
Это простое решение, в котором не нужны даже координаты точки C.
Можно решать сложно, определяя координаты точке M и N и вычисляя затем длину отрезка MN по координатам:
Координаты середины отрезка равны полусумме соответствующих координат концов отрезка.
Точка M (середина AC):
x=(-1+3)/2=1
y=(2+(-2))/2=0
z=(3+1)/2=2
M(1;0;2)
Точка N (середина BC):
x=(1+3)/2=2
y=(0+(-2))/2=-1
z=(4+1)/2=5/2
N(2;-1;5/2)
MN² = (2-1)²+(-1-0)²+((5/2)-2) = 1+1+1/4 = 9/4 = (3/2)²
|MN| = 3/2
ответ, разумеется, такой же: длина MN равна 1,5.