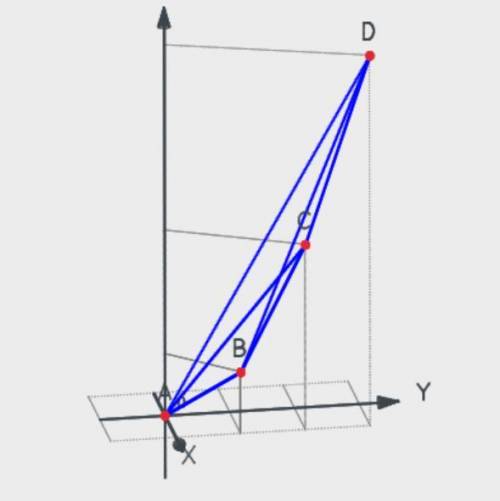
Даны координаты вершин тетраэдра АВСD :
A(0, 0, 0), B(1, 1, 1) , C(1, 2, 3, D(1, 3, 6).
А) Площадь основания АВС.
Находим векторы АВ и АС.
АВ = (1; 1; 1), АС = (1; 2; 3).
Их векторное произведение равно.
i j k | i j
1 1 1 | 1 1
1 2 3 | 1 2 = 3i + 1j + 2k - 3j - 2i - 1k = 1i - 2j + 1k.
Нормальный вектор к плоскости АВС равен (1; -2; 1).
Площадь АВС равна половине модуля векторного произведения:
S = (1/2)*√(1 + 4 + 1) = √6/2 ≈ 1,225.
Б) Уравнение высоты тетраэдра DК.
Её направляющий вектор найден - он равен нормальному вектору плоскости АВС(1; -2; 1).
Используем координаты точки D.
Уравнение прямой DК: (x – 1)/1 = (y – 3)/(-2) = (z – 6)/1.
В) Уравнение прямой, проходящей через точку С параллельно DК.
Её направляющий вектор найден равен направляющему вектору высоты DК.
Осталось подставить координаты точки С.
Уравнение прямой СР: (x – 1)/1 = (y – 2)/(-2) = (z – 3)/1.
Г) Расстояние от точки С до грани ABD.
Пусть точка М – проекция точки С на плоскость ABD.
Находим векторы АВ и АD.
АВ = (1; 1; 1), АD = (1; 3; 6).
Их векторное произведение равно.
i j k | i j
1 1 1 | 1 1
1 3 6 | 1 3 = 6i + 1j + 3k - 6j - 3i - 1k = 3i - 5j + 2k.
Площадь грани ABD равна половине модуля полученного векторного произведения.
S(ABD) = (1/2)*√(9 + 25 + 4) = (1/2)√38.
Полученный вектор (3; -5; 2) – это вектор нормали к плоскости АВD, то есть высоты СМ.
Получаем уравнение высоты СМ: (x – 1)/3 = (y – 2)/(-5) = (z – 3)/2.
Находим объём пирамиды как (1/6) модуля смешанного произведения векторов АВ и АС (1; -2; 1) на AD (1; 3; 6)..
V = (1/6)*(1 –6 + 6) = (1/6) куб.ед.
Тогда длина высоты СМ равна:
h(CM) = 3V/S(ABD) = (3*(1/6))/( (1/2)√38) =1/√38 = √38/38 ≈ 0,162.
Д) Уравнение плоскости, проходящей через точки В и С перпендикулярно плоскости АВС.
Если через точки В и С провести прямые с направляющим вектором как у высоты DK, то получим 2 параллельные прямые, перпендикулярные плоскости АВС.
Одна прямая уже известна – это СР: (x – 1)/1 = (y – 2)/(-2) = (z – 3)/1.
Аналогична прямая через точку В – это ВТ: (x – 1)/1 = (y – 1)/(-2) = (z – 1)/1.
Найдём точку на прямой СР. Для этого уравнение прямой представим в параметрическом виде.
СР: (x – 1)/1 = (y – 2)/(-2) = (z – 3)/1 = t.
x = t + 1,
y = -2t + 2,
z = t + 3.
Примем t = 1, тогда x = 2, y = 0, z = 4. Пусть это координаты точки Р.
Имеем 3 точки В, С, и Р, через которые проведём искомую плоскость.
x – x1 y – y1 z – z1
x2 – x1 y2 – y1 z2 – z1
x3 – x1 y3 – y1 z2 – z1.
Подставим координаты точек.
x -1 y – 1 z – 1 | x – 1 y – 1
1 – 1 2 – 1 3 – 1 | 1 – 1 2 – 1
2 – 1 0 – 1 4 – 1 | 2 – 1 0 – 1
x -1 y – 1 z – 1 | x – 1 y – 1
0 1 2 | 0 1
1 – 1 3 | 1 – 1 =
= 3(x – 1) + 2(y – 1) – 0 – 0 + 2(x – 1) – 1(z – 1) = 3x – 3 + 2y – 2 + 2x – 2 – 1z + 1 =
= 5x + 2y - 1z – 6=0.
Е) Длина ребра BD.
Вектор BD = (0; 2; 5). Его модуль (длина) равен √(0² + 2² + 5²) = √29 ≈ 5,385.
Ж) Объём пирамиды найден в пункте В.
V = (1/6) куб.ед.
З) Угол при вершине С грани BCD.
Находим векторы:
СВ = (0; -1; -2), модуль равен √(0² + (-1)² + (-2)²) = √5.
CD = (0; 1; 3), модуль равен √(0² + 1² + 3²) = √10.
Их скалярное произведение равно:
СВ х CD = 0 – 1 – 6 = -7.
cos C = -7/(√5*√10) = -7/√50 ≈ -0,989949.
Угол С равен arc cos (-0,989949) = 2,999696 радиан или 171,8699 градуса.
И) Угол между ребром CD и плоскостью АВС.
Вектор CD = (0; 1; 3), нормальный вектор к плоскости АВС равен (1; -2; 1) (найдены ранее).
угол между этой прямой и плоскостью
sin φ = | A • l + B • m + C • n |
√(A² + B² + C²) • √(l² + m² + n²)
Направляющий вектор прямой имеет вид: s = {l; m; n}.
Вектор нормали плоскости имеет вид: Ax + By + Cz + D = 0.
sin φ = (1*0 – 2*1 + 1*3)/( √6*√10) = 1/√60 ≈ 0,129.
φ = arc sin (1/√60) = 0,129 радиан или 7,418 градуса.
M(0; -8·√3; 8)
Пошаговое объяснение:
Пусть r радиус-вектор точки M(x; y; z). По условию |r| = 16.
Радиус-вектор точки M(x; y; z) составляет с осью OX угол 90° и поэтому находится полностью на плоскости OYZ и поэтому x=0.
Радиус-вектор точки M составляет с осью OY угол 150° (этот угол считается против часовой стрелки), что означает y<0 и составляет с осью OY угол по часовой стрелки 180°-150°=30° и составляет с осью OZ угол против часовой стрелки 180°-30°=60°. Тогда проекция радиуса-вектора на ось OY равна:
-y= |r|· cos30°= 16·√3/2=8·√3.
а проекция радиуса-вектора на ось OZ равна:
z= |r|· cos60°= 16·1/2=8.