а) Раз треугольники подобны, то их стороны по определению пропорциональны.
Давайте для наглядности обозначим эти два треугольника буквами : первый пускай будет △ABC, а второй — △DEF. В таком случае можно сделать такую запись: △ABC ~ △DEF (знак тильда должен находиться на уровне букв).
Теперь составляем такую запись :
Подставляем известные стороны :
И вычисяем две неизвестные стороны второго треугольника :
1 :
м
м
2 (через коэффициент пропорциональности) :
м
м
ответ : Остальные две стороны второго треугольника равны 308 м и 209 м.
б) P(△ABC) = 45 + 56 + 38 = 139 м
P(△DEF) = 308 + 247,5 + 209 = 764,5 м
ответ : Периметры участков отличаются в 5,5 раз (тот же коэффициент пропорциональности).
Приведем однородные члены: 4A + 4B + 4C + 4E + 4D = 1156 4(A + B + C + E + D) = 1156 A + B + C + E + D = 1156 : 4 A + B + C + E + D = 289 г.
Видим, что в левой части равенства сумма масс всех монет, значит, сумма масс всех монет равна 289 г.
ответ: 289 г.
2-й : Можно прикинуть еще так: Найдем среднее арифметическое масс пар монет: Всего пар 10: (110+112+113+114+115+116+117+118+120+121):10= = 1156:10 = 115,6 г
Значит, можно найти среднее арифметическое массы одной монеты 115,6 : 2 = 57,8 г
Но всего рассматривается 5 монет. Умножим 5 на среднюю массу одной монеты и узнаем массу всех пяти монет. 57,8 • 5 = 289 г.
а) 308 м, 247,5 м, 209м
б) В 5,5 раз.
Пошаговое объяснение:
а) Раз треугольники подобны, то их стороны по определению пропорциональны.
Давайте для наглядности обозначим эти два треугольника буквами : первый пускай будет △ABC, а второй — △DEF. В таком случае можно сделать такую запись: △ABC ~ △DEF (знак тильда должен находиться на уровне букв).
Теперь составляем такую запись :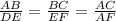
Подставляем известные стороны :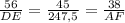
И вычисяем две неизвестные стороны второго треугольника :
1 :
2 (через коэффициент пропорциональности) :
ответ : Остальные две стороны второго треугольника равны 308 м и 209 м.
б) P(△ABC) = 45 + 56 + 38 = 139 м
P(△DEF) = 308 + 247,5 + 209 = 764,5 м
ответ : Периметры участков отличаются в 5,5 раз (тот же коэффициент пропорциональности).