4/(4+2√3) cм² - площадь вписанного квадрата
Пошаговое объяснение:
Вписанный квадрат отсекает от заданного квадрата 4 прямоугольных и равных между собой треугольника с острыми углами 60° и 30°.
Пусть сторона вписанного квадрата = х см. Тогда части стороны большого квадрата равны:
х/2 см - катет, лежащий против угла в 30°,
по теореме Пифагора, катет, лежащий против угла в 60° равен:
√(x² - x²/4) = x√3/2 см
Сторона заданного квадрата равна сумме этих катетов:
x/2 + x√3/2 = 1
x + x√3 = 2
x = 2/(1+√3) - сторона вписанного квадрата
S вписанного квадрата = x² = 2²/(1+√3)² = 4/(1+√3)² = 4/(4+2√3) cм²
Пошаговое объяснение:
рассмотрим треугольник АВО:
ВО - высота, ВО = 6 см, угол А = 30 градусам, угол АОВ = 90 градусов,
ВО - катет противолежащего угла А = 30 градусам равен половине гипотенузы АВ. АВ = 2ВО, АВ = 2*6=12 см.
Рассмотрим треугольник ОВС:
АО=ОС - по условию, АО, ОС - катеты треугольников АВО, ОВС.
ВО - катет треугольника ОВС.
угол ВОС = 90 градусов.
Треугольник АВО = треугольнику ОВС. ПО первому признаку равенства треугольников: если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
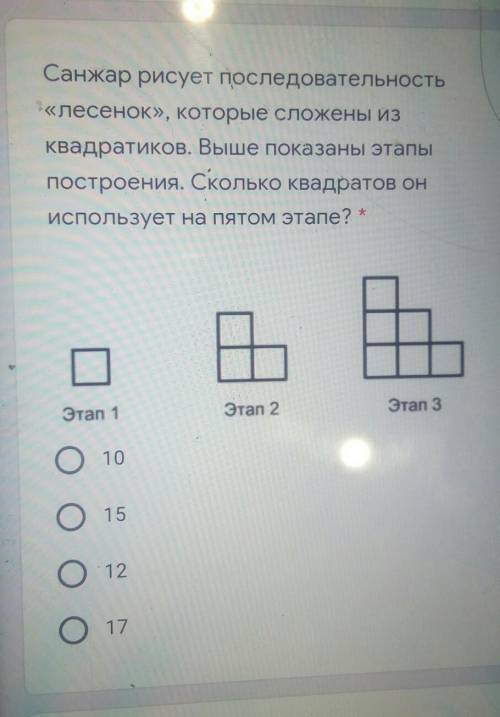
ответ:15
Пошаговое объяснение:
На пятом этапе к 10 квадратам, имеющимся после четвертого этапа, добавится еще 5, итого их станет 15.