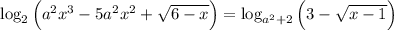
Раз некоторое число  удовлетворяет уравнению при любом
удовлетворяет уравнению при любом  , то оно также удовлетворяет уравнению при
, то оно также удовлетворяет уравнению при 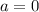 .
.
То есть, если мы подставим в уравнение 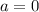 , то выполнится равенство:
, то выполнится равенство:
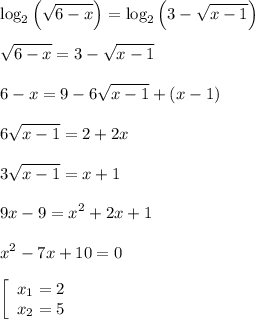
Оба корня удовлетворяют уравнению и ОДЗ (при 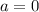 ): с обеих сторон в первом случае получается
): с обеих сторон в первом случае получается  , а во втором
, а во втором 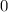 (так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
(так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при 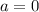 . И если ответ на задачу существует, то он может быть только
. И если ответ на задачу существует, то он может быть только 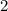 ,
, 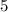 или и
или и 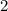 , и
, и 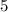 . Но про другие значения
. Но про другие значения  мы пока ничего не знаем.
мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при 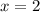 :
:
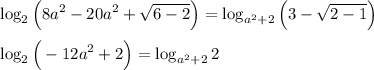
Вот только первый логарифм не всегда существует. 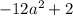 может быть отрицательным (возьмите, к примеру,
может быть отрицательным (возьмите, к примеру, 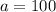 ). А подлогарифмическое выражение обязано быть положительным. Значит, такой
). А подлогарифмическое выражение обязано быть положительным. Значит, такой  нас не устраивает.
нас не устраивает.
Теперь проверим 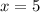 :
:
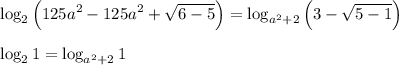
В обеих частях мы получили 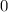 (так как
(так как 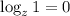 , если
, если 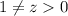 ). Также
). Также 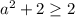 , поэтому все ограничения будут выполняться.
, поэтому все ограничения будут выполняться.
В итоге имеем нужный ответ: 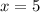 .
.
Задача решена!
первым делом решаются скобки:
1)-0.25-3/4-1/2
мы видим разность дробей с разными знаменателями, чтобы выполнить это действие, нужно привести все дроби к одному знаменателю, в данном случае это 4.
-1/4-3/4-2/4=-6/4=-3/2
2) далее выполняем умножение:
-3/2*(-0,2)
дроби умножаются БЕЗ приведения к общему знаменателю, а умножение минуса на минус даёт плюс:
-3/2*(-2/10)=6/20=3/10
3)видим сумму, знаменатель одинаковый, значит можем спокойно складывать числители, переведя 3,9 в неправильную дробь:
3/10+3,9=3/10+39/10=42/10=4,2
Пасмурные дни 30*1/10=3
переменная облачность 30*3/10=9
осадки 30*1/10=3
солнечные дни 30*1/2=15
В апреле 30 дней
3+9+3+15=30
Больше всего солнечных дней.
Меньше всего пасмурных и осадков.
Солнечных дней больше, чем пасмурных.