Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a. После первой выплаты сумма долга составит: S1 = Sb − X. После второй выплаты сумма долга составит: S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X. После третьей выплаты сумма оставшегося долга равна: S3 = Sb³ - (1-b+b²)X = Sb³ - · X После четвертой выплаты сумма оставшегося долга равна: S4 = - (1 + b +b² + b³)X = - · X По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому - · X = 0. Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается: X = рублей
Літо - моя сама улюблена пора року. нарешті-те закінчуються холоди й починаються канікули. улітку можна радуватися сонцю й теплим денькам, відправлятися в далекі подорожі й походи. особливо прекрасна влітку природа - шумить зеленими листами ліс, поспівають ягоди, розцвітають самі дивні квіти. можна нескінченно гуляти по квітучих лугах і любуватися на скромні білоголові ромашки або плести вінки з кульбаб. приємно зайти в сутінок лісу й зникнути від денної спеки. а якщо придивитися уважно, те нагородою за лісову прогулянку будуть коричневі міцні боровики й горді красноголовці
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.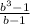 · X
· X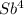 - (1 + b +b² + b³)X =
- (1 + b +b² + b³)X = 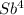 -
- 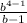 · X
· X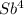 -
- 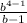 · X = 0.
· X = 0. рублей
рублей
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -
После четвертой выплаты сумма оставшегося долга равна:
S4 =
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X =