Подобные уравнения решаются с замены переменной.
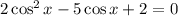
Заменим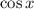 
на t (буква может быть любая, но эта привычнее).
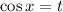
Тогда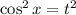 
Так как косинус может принимать значения только из отрезка [-1; 1], то и t должно удовлетворять этому требованию:
![t\in[-1;\;1]](/tpl/images/1214/5114/1ab10.png)
Подставим данные значения в исходное уравнение и решим его как квадратное в отношении t:
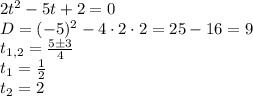
Второй корень не подходит, т.к.
Выполним обратную замену переменной и найдём x:
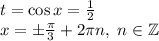
ответ: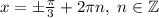 
P.S. Если оба корня квадратного уравнения лежат в отрезке [-1; 1], обратную замену производим для каждого корня. В ответе к задаче также будет два корня.
1) -2 1/2÷3 1/3=-5/2÷10/3=-5/2×3/10=-15/20=-3/4
2) -4 2/3÷(-1 1/6)=4 2/3÷1 1/6=14/3÷7/6=14/3×6/7=84/21=4
3) 3 3/8÷(-2 1/4)=-3 3/8÷2 1/4=-27/8÷9/4=-27/8×4/9=-108/72=-3/2=-1 1/2
4) -7 1/2÷3 3/4=-15/2÷15/4=-15/2×4/15=-60/30=-2