z = (x-2)^2+2*y^2-10
1. Найдем частные производные.
На фото
2. Решим систему уравнений.
2*x-4 = 0
4*y = 0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = 2
4*y = 0
Откуда y = 0
Данные значения y подставляем в выражение для x. Получаем: x = 2
Количество критических точек равно 1.
M1(2;0)
3. Найдем частные производные второго порядка.
На фото
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(2;0)
На фото
AC - B2 = 8 > 0 и A > 0 , то в точке M1(2;0) имеется минимум z(2;0) = -10
Вывод: В точке M1(2;0) имеется минимум z(2;0) = -10;
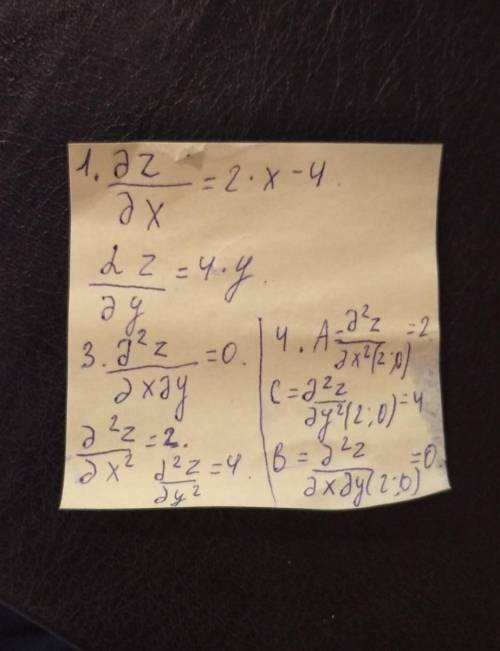
z = (x-2)^2+2*y^2-10
1. Найдем частные производные.
На фото
2. Решим систему уравнений.
2*x-4 = 0
4*y = 0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = 2
4*y = 0
Откуда y = 0
Данные значения y подставляем в выражение для x. Получаем: x = 2
Количество критических точек равно 1.
M1(2;0)
3. Найдем частные производные второго порядка.
На фото
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(2;0)
На фото
AC - B2 = 8 > 0 и A > 0 , то в точке M1(2;0) имеется минимум z(2;0) = -10
Вывод: В точке M1(2;0) имеется минимум z(2;0) = -10;
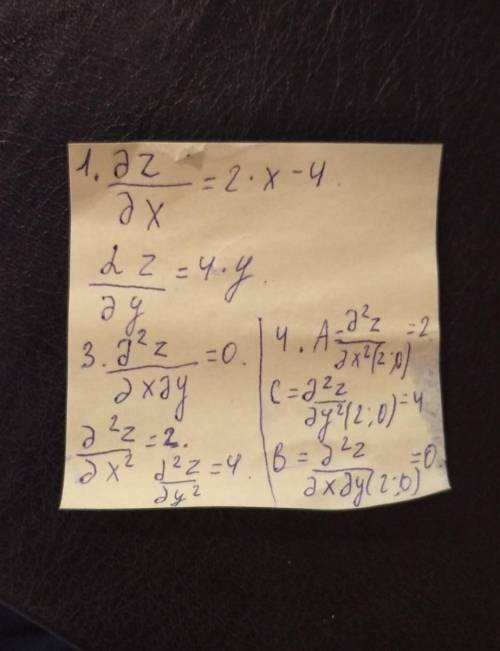
Пошаговое объяснение:
а) (3,6-Х)*5,8=14,5
3,6-х=14,5/5,8
3,6-х=2,5
-х=2,5-3,6
-х=-1,1
х=1,1
б) 12,98-(3,8х-1,3х)=11,23
2,5х=11,23-12,98
2,5х=-1,75
х=-1,75/2,5
х=-0,7