Пошаговое объяснение:
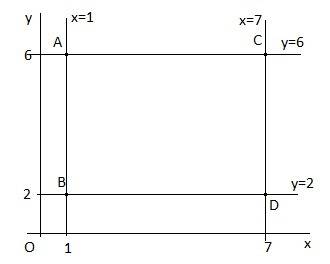
Отметим точки A, B и C на координатной плоскости. У точек A и B совпадают абсциссы точек, соединяем их прямой x = 1.
У точек A и C совпадают ординаты точек, соединяем их прямой y = 6.
Через точку B с ординатой 2 проводим прямую y = 2 параллельную прямой y = 6 (противоположной стороне прямоугольника).
Через точку C с абсциссой 7 проводим прямую x = 7 параллельную прямой x = 1 (противоположной стороне прямоугольника).
Проведенные через точки B и C прямые пересекутся в точке D(7; 2), которая и будет 4 вершиной прямоугольника ABCD.
Если А(х), а В(у), рассояние АВ=|x-y|.
АВ=|x +1-(х-3) |= |x +1-х+3 |x= |4|=4
АС= |x+1-(2х+3) |= |x +1-2х-3 |= |-x-2 |= |x +2 |.
Т. к. АВ=АС, то решим уравнение: |x +2 |=4.
х+2=4 или х+2=-4,
х=2 или х=-6.