Пошаговое объяснение:
у₁ = - х² + 3х,
у₂ = - х² +9;
х = -2; х = 2; у =0
общая формула расчета площади фигур, ограниченных кривыми y₁(x) и y₂(x) имеет вид
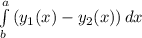
(здесь следует отметить, что если при расчете определенного интеграла получилась отрицательная величина - не стоит пугаться, поскольку мы считаем площадь, нужно просто в ответе поменять
знак - на +)
но после того, как мы нарисуем чертежи, мы увидим, что у нас есть две фигуры (они закрашены желтым)
поэтому у нас будет S = S₁ + S₂
интервалы интегрирования будут для S₁ -2 ≤x≤3 и для S₂ 3≤x4
так и рассчитаем
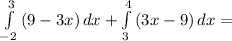
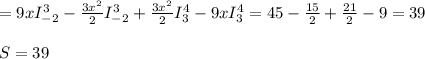
k = - 14; x₂=3.
Пошаговое объяснение:
1) Найдём k, для чего подставим в исходное уравнение вместо одного из известных корней его значение:
2* 4² + k*4 + 24 = 0,
откуда
4k = - 24 - 32 = - 56,
k = - 14.
2) Составляем уравнение, в котором k = - 14, и находим оба корня.
2x²- 14x+24=0
Дискриминант данного уравнения равен:
D = b² - 4ac = (-14)2-4·2·24 = 196-192 = 4
Так как дискриминант больше нуля, то это означает, что данное квадратное уравнение имеет два действительных корня. Находим их:
x₁=14+√b²)/(2*2)= (14+2)/4=16/4= 4 - этот корень был задан как известный;
x₂=(14-√b²)/(2*2)= (14-2)/4 =12/4=3 - это второй корень, который мы нашли.
ответ: k = - 14; x₂=3.