Question

Найти сумму коэффициентов a+с квадратного трехчлена ax2+2x+c, если x=2 и x=-4, корни данного трехчлена.

Answer 1

Поскольку известны корни трехчлена, то верны следующие равенства:

$\left \{ {{a*(2)^2+2*2+c=0} \atop {a*(-4)^2+2*(-4)+c=0}} \right.$

Преобразовываем оба уравнения:

$\left \{ {{4a+4+c=0} \atop {16a-8+c=0}} \right.$

Вычитаем второе из первого:

$16a-8+c- (4a+4+c)=0$

Приводим подобные:

$12a-12=0$, отсюда $a=1$

Подставляем a в одно из уравнений, например, в первое:

$4+4+c=0$, откуда $c=-8$

Тогда $a+c = 1+(-8)=-7$

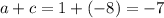
По теореме Виета, для квадратного уравнения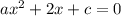 $ax^2+2x+c=0$, если 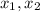$x_1,x_2$ - корни уравнения, то верно следующее:

$\left \{ {{x_1+x_2=-\frac{2}{a}} \atop {x_1x_2=\frac{c}{a}}} \right.$

(правая часть первого уравнения - коэффициент при x, деленный на коэффициент при старшей степени, т.е. a, взятый со знаком минус, правая часть второго уравнения - свободный коэффициент, то бишь c, деленный на коэффициент при старшей степени, то бишь a)

Поскольку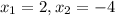 $x_1=2,x_2=-4$, то получаем:

$\left \{ {{2+(-4)=-\frac{2}{a}} \atop {2*(-4)=\frac{c}{a}}} \right.$

Из первого уравнения находим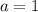 $a=1$. Подставляем a во второе уравнение, находим, что 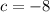$c=-8$. Наконец, находим сумму:

$a+c = 1+(-8)=-7$

Эпилог

Двумя получили одинаковый результат, и это хорошо.