Пусть х - собственная скорость лодки. По течению моторная лодка плыла со скоростью:
v(по теч.)=v(собств.) + v(теч.)=х+4 км/час
Против течения моторная лодка плыла со скоростью:
v(пр. теч.)=v(собств.) - v(теч.)=х-4 км/час
Время в пути по течению равно: t(по теч.) =S÷v(по теч.)=221/(х+4) часа
Время в пути против течения равно: t(пр. теч.) =S÷v(пр. теч.)=221/(х-4) часа.
На путь по течению ушло на 2 часа меньше времени, чем по течению.
Составим и решим уравнение:
221/(х-4) - 221/(х+4)=2 (умножим на (х-4)(х+4), чтобы избавиться от дробей)
221×(х-4)(х+4)/(х-4) - 221×(х+4)(х-4)/(х+4)=2(х+4)(х-4)
221(х+4) - 221(х-4)=2(х²-16)
221х+884 - 221х+884=2х²-32
1768=2х²-32
2х²=1768+32
2х²=1800
х²=1800÷2
х²=900
х=±√900
х₁=-30 (не подходит, т.к. х₁<0 (-30)²=900)
х₂=30 (км/час) - скорость лодки в неподвижной воде
Пусть х - собственная скорость лодки. По течению моторная лодка плыла со скоростью:
v(по теч.)=v(собств.) + v(теч.)=х+4 км/час
Против течения моторная лодка плыла со скоростью:
v(пр. теч.)=v(собств.) - v(теч.)=х-4 км/час
Время в пути по течению равно: t(по теч.) =S÷v(по теч.)=221/(х+4) часа
Время в пути против течения равно: t(пр. теч.) =S÷v(пр. теч.)=221/(х-4) часа.
На путь по течению ушло на 2 часа меньше времени, чем по течению.
Составим и решим уравнение:
221/(х-4) - 221/(х+4)=2 (умножим на (х-4)(х+4), чтобы избавиться от дробей)
221×(х-4)(х+4)/(х-4) - 221×(х+4)(х-4)/(х+4)=2(х+4)(х-4)
221(х+4) - 221(х-4)=2(х²-16)
221х+884 - 221х+884=2х²-32
1768=2х²-32
2х²=1768+32
2х²=1800
х²=1800÷2
х²=900
х=±√900
х₁=-30 (не подходит, т.к. х₁<0 (-30)²=900)
х₂=30 (км/час) - скорость лодки в неподвижной воде
Возьмем, к примеру, кубик со стороной
. Его объем равен 
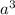. Если мы сторону кубика увеличим в n раз, то сторона кубика станет равной 
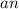. Тогда его объем будет равен 
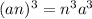. Видно, что если поделить объем кубика со стороной 
на объем кубика со стороной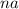 
, то получим 
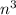. Именно во столько раз изменится объем.
Аналогично можно проделать рассуждения для шара. При увеличении радиуса в n раз объем шара увеличится в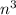
раз.
Для параллелепипеда с увеличением всех сторон в n раз его объем увеличится в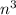
раз.
Вообще, для тела произвольной формы эта закономерность сохраняется. Нестрого говоря, любое тело можно разбить на кубики (чем меньше сторона кубика, тем точнее можно описать произвольное тело), и, поскольку у каждого кубика объем увеличивается в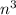
раз, то и объем всего тела увеличится также.