1)
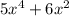
2)
функция - не монотонная
экстремумы: (-6; 540), (8; -832)
3)
минимум f(4)= -1
максимум f(2)=3
Пошаговое объяснение:
1)
просто диференцируем по частям
2)
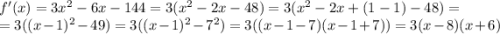
это производная исходной функции
как бы тут уже видно, что производная:
квадратичная парабола,
роги вверх,
знак меняет (а это значит, что исходная функция - не монотонная) в точках: x1 = -6; x2 = 8. это и будут точки экстремумов
минимум и максимум производной нас не интересуют
Решаем уравнение
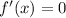
3(x-8)(x+6) = 0
x1 = -6
x2 = 8
y1 = 540 = (-6)³ -3*(-6)² - 144*(-6) = -216 -108 + 864 = -324 + 864 = 540
y2 = -832 = 8³ -3*8² -144*8 = 8*64 - 3*64 - 144*8 = 5*8*8 - 144*8 =
= 8*(40-144) = 8*(-104) = -800 -32= -832
3)
f(2) = 4-16+15 = 3
f(5) = 25 -40 +15 =0
f'(x) = 2x-8
f'(x) = 0 при х = 4
f(4) = 16 - 32 +15 = -1
из f(2)=3, f(4)= -1, f(5)=0 выбираем минимум и максимум
минимум f(4)= -1
максимум f(2)=3
прим.: на втором таки уткнулся. противно его считать в голове. по быстрому там тупо решается квадратное уравнение через дискриминант на листике
1)
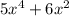
2)
функция - не монотонная
экстремумы: (-6; 540), (8; -832)
3)
минимум f(4)= -1
максимум f(2)=3
Пошаговое объяснение:
1)
просто диференцируем по частям
2)
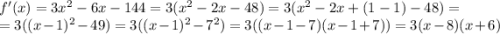
это производная исходной функции
как бы тут уже видно, что производная:
квадратичная парабола,
роги вверх,
знак меняет (а это значит, что исходная функция - не монотонная) в точках: x1 = -6; x2 = 8. это и будут точки экстремумов
минимум и максимум производной нас не интересуют
Решаем уравнение
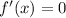
3(x-8)(x+6) = 0
x1 = -6
x2 = 8
y1 = 540 = (-6)³ -3*(-6)² - 144*(-6) = -216 -108 + 864 = -324 + 864 = 540
y2 = -832 = 8³ -3*8² -144*8 = 8*64 - 3*64 - 144*8 = 5*8*8 - 144*8 =
= 8*(40-144) = 8*(-104) = -800 -32= -832
3)
f(2) = 4-16+15 = 3
f(5) = 25 -40 +15 =0
f'(x) = 2x-8
f'(x) = 0 при х = 4
f(4) = 16 - 32 +15 = -1
из f(2)=3, f(4)= -1, f(5)=0 выбираем минимум и максимум
минимум f(4)= -1
максимум f(2)=3
прим.: на втором таки уткнулся. противно его считать в голове. по быстрому там тупо решается квадратное уравнение через дискриминант на листике
Доказано
Пошаговое объяснение:
Пронумеруем числа по порядку - x1 x2 x3 , пойдём от обратного - докажем что есть круг, в котором есть различные числа, и он удволетворяет данному правилу. x1 < x2 < x3. ( (x1+x3)/2 = x2) продолжим круг. x2 < x3 <x4. Продолжим по той же схеме, и получим, что x2020 будет > x2019 > x2018
соответственно (x2020 + x2)/2 = x1 (Потому что это круг)
Напомним, что x2>x1 и x2020 > x1. Можно представить, что x2 = x1 + k, а x2020 = x1 + n
тогда (x2020 + x2)/2 = (2*х1 +k + n) /2 = x1 + (k+n)/2. Так как k и n > 0 то поучим что x1 = x1 + (k+n)/2. А мы уточнили, что они оба положительные, и быть 0 не могут. Следовательно - такого быть не может. Значит и всё утверждение(выделено) тоже не верно.