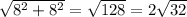, а сторона основания равна удвоенному катету, лежащему на этом основании, то есть 8*2=16, тогда площадь одной боковой грани равна 
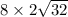, а площадь всех боковых граней равна сумме четырех этих площадей. В свою очередь полная площадь равна сумме площади боковых граней и площади основания, где площадь основания равна 16*16=4^4=2^8=256, поэтому площадь полной поверхности равна 
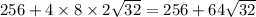Будем надеяться, что я не ошибся в вычислениях.
Пусть площадь поля, засеянного овсом - х,
тогда площадь поля, засеянного пшеницей - 2х.
Общая площадь поля - у.
2 год:
Площадь поля, засеянного овсом - 2х +20%, или 2х+0,2х;
Площадь поля, засеянного пшеницей - х+15%, или х+0,15х.
Общая площадь поля - у+11.
Составим систему уравнений:
х+2х=у
2х+0,2х+х+0,15х=у+15.
Подставим во 2е уровнения вместо у выражение:
2х+0,2х+х+0,15х=х+2х+11
Решаем
2х+0,2х+х+0,15х-х-2х=11
0,35х=11
х=11/0,35
х=31,43
Вычислим у:
у=х+2х
у=31,43+2*31,43
у=94,29 (общая площадь поля в первом году)
Во втором году на 11 га больше, соответственно:
94,29+11=105,29 га - площадь поля, засеянного пшеницей и овсом на следующий год