2+2 = 4.
Надеюсь смог
- 3/5
Пошаговое объяснение:
cos (pi/2 + A) при cos А = 4/5 и А∈(3*pi/2; 2*pi)
cos (pi/2 + A) = - sin A (по формулам приведения)
Угол A∈(3*pi/2; 2*pi), это - 4 четверть, где синус имеет отрицательный знак.
По основному тригонометрическому тождеству
cos A ^ 2 + sin A ^ 2 = 1
имеем:
sin A ^ 2 = 1 - cos A ^ 2
sin A ^ 2 = 1 - (4/5) ^ 2 = 1 - 16/25 = 25/25 - 16/25 = 9/25
Значит, с учётом знака
sin A = - 3/5
№ 4. x ≤ 0.75
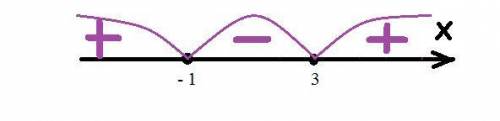
№ 5. ( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пошаговое объяснение:
№ 4. 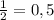
Тогда выражение имеет вид:
(0,5)^ (2*x) ≥ (0.125) ^ (1/2)
(0.5) ^ (2*x) ≥ ((0.5)^3)^(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3*(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3/2)
(0.5) ^ (2*x) ≥ (0.5) ^ 1.5
Т.к. 0,5 < 1, то имеем:
2 * х ≤ 1.5
x ≤ 1.5 / 2
x ≤ 0.75 или иначе записать можно так х ≤ 
№ 5. 7 ^ (x ^ 2) * 49 ^ ( - x) ≥ 343
7 ^ (x ^ 2) * 7^2^ ( - x) ≥ 7 ^ 3
7 ^ (x ^ 2) * 7^ ( - 2 * x) ≥ 7 ^ 3
7 ^ ((x ^ 2) + ( - 2 * x)) ≥ 7 ^ 3
7 ^ (x ^ 2 - 2 * x) ≥ 7 ^ 3
Т.к. 7 > 1, то запишем так:
x ^ 2 - 2 * x ≥ 3
Решим получившееся квадратное неравенство.
x ^ 2 - 2 * x = 3
x ^ 2 - 2 * x - 3 = 0
D = 16
x1,2 = (2±4)/2
x1 = 3 и x2 = -1
Решим методом интервалов.
( - ∞; - 1 ] ∪ [ 3; + ∞ )
4
Пошаговое объяснение:
ВАУ